《2025年一本通武汉出版社九年级数学上册北师大版核心板》

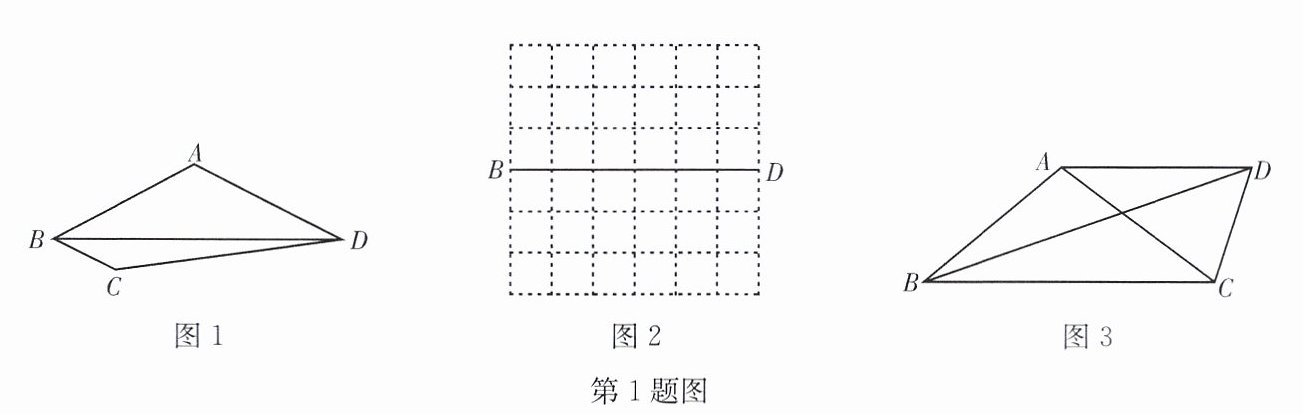
1. 若一个四边形有一组邻边相等,且这组邻边夹角所对的对角线平分一个内角,则称这样的四边形为“近似菱形”。例如：如图1,在四边形ABCD中,AB= AD,BD平分∠ABC,则四边形ABCD是“近似菱形”。
(1)请在图2中作出一个以BD为对角线的“近似菱形”ABCD,顶点A,C要在网格的格点上；
(2)如图3,在四边形ABCD中,AB= AC,AD//BC,∠CAD= 2∠DBC,求证：四边形ABCD是“近似菱形”；
(3)在(2)的条件下,若BD= 3,CD= 1,求AB的长。

答案：
(1) 作图（略，需在图2网格中以BD为对角线，作出邻边相等且对角线平分内角的四边形，顶点A、C在格点上）。
(2) 证明：设∠DBC = α，则∠CAD = 2α。
∵ AD//BC，
∴ ∠ADB = ∠DBC = α。
∵ AB = AC，设∠ABC = ∠ACB = β。
在△ABD中，∠ABD = β - α，∠BAD = 180° - (β - α) - α = 180° - β。
在△ABC中，∠BAC = 180° - 2β，
∴ ∠CAD = ∠BAD - ∠BAC = (180° - β) - (180° - 2β) = β。
又∠CAD = 2α，
∴ β = 2α，即∠ABC = 2α，∠ABD = α = ∠DBC。
∴ BD平分∠ABC，且AB = AC（一组邻边相等）。
∴ 四边形ABCD是“近似菱形”。
(3) 解：设AB = AC = x，BC = y。
由AD//BC，可证△AOD∽△COB（O为AC、BD交点），设AO = 2k，OC = k，则AC = 3k = x，AO = 2x/3，OC = x/3。
BD = 3，设BO = m，OD = 3 - m，由相似比得OD/BO = AO/OC = 2，即(3 - m)/m = 2，解得m = 1，BO = 1，OD = 2。
在△ABO和△CBO中，由角平分线定理：AB/BC = AO/OC = 2，即x/y = 2，y = x/2。
在△BOC中，由余弦定理：OC² = BO² + BC² - 2·BO·BC·cosα，即(x/3)² = 1² + (x/2)² - 2·1·(x/2)·cosα ①
在△ABC中，cosβ = cos2α = 2cos²α - 1，由余弦定理：cosβ = (AB² + BC² - AC²)/(2·AB·BC) = (x² + (x/2)² - x²)/(2·x·x/2) = 1/4。
∴ 2cos²α - 1 = 1/4，解得cosα = √10/4（取正值）。
代入①：x²/9 = 1 + x²/4 - 2·1·(x/2)·(√10/4)，整理得5x² - 9√10 x + 36 = 0，解得x = √10（舍负）。
∴ AB = √10。