《2025年一本通武汉出版社九年级数学上册北师大版核心板》

1. 两个相似三角形对应角平分线的比为3:4,则对应中线的比为 …………………… (A)
A.3:4
B.9:16
C.$\sqrt{3}:2$
D.4:3

答案： 【解析】：
本题考查了相似三角形的性质。在相似三角形中，对应角平分线的比、对应中线的比、对应高的比以及相似比都是相等的。题目中已给出两个相似三角形对应角平分线的比为$3:4$，因此，可以直接推断出对应中线的比也为$3:4$。
【答案】：
A

2. 如图,$\triangle ADE \backsim \triangle ABC$,相似比为1:3,则$AF:AG$为 …………… (A)
A.1:3
B.3:1
C.1:9
D.9:1

答案： 【解析】：
本题可根据相似三角形的性质来求解$AF$与$AG$的比值。
已知$\triangle ADE\sim\triangle ABC$，相似比为$1:3$。
相似三角形对应高的比等于相似比，在$\triangle ADE$和$\triangle ABC$中，$AF$是$\triangle ADE$中$AD$边上的高，$AG$是$\triangle ABC$中$AB$边上的高，且$AD$与$AB$是对应边，所以$AF:AG$等于相似比$1:3$。
【答案】：A

3. 若两个相似三角形的相似比是2:3,则它们的对应高线的比为2:3,对应中线的比为2:3,对应角平分线的比为2:3.

答案： 【解析】：
本题主要考查相似三角形的性质。
根据相似三角形的性质，如果两个三角形是相似的，并且它们的相似比是$k$，
那么它们的对应高线、对应中线、对应角平分线的比也都等于$k$。
在本题中，两个相似三角形的相似比是$2:3$，
因此，可以直接应用相似三角形的性质来求解。
【答案】：
对应高线的比为$2:3$；
对应中线的比为$2:3$；
对应角平分线的比为$2:3$。

4. 如图,$\triangle ABC与\triangle A'B'C'$相似,$AD,BE是\triangle ABC$的高,$A'D',B'E'是\triangle A'B'C'$的高.
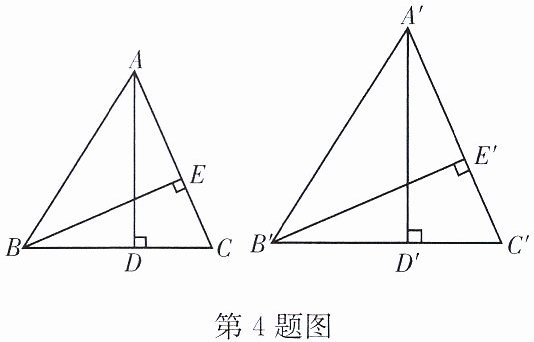
求证:$\frac{AD}{A'D'}= \frac{BE}{B'E'}$.

答案： 【解析】：本题主要考查相似三角形的性质，即相似三角形对应高的比等于相似比。我们可以通过证明两个三角形分别以$AD$、$A'D'$和$BE$、$B'E'$为高的两个直角三角形相似，进而得出对应高的比相等。
【答案】：证明：
∵$\triangle ABC\sim\triangle A'B'C'$，
∴$\frac{AB}{A'B'}=\frac{BC}{B'C'}$，$\angle B = \angle B'$（相似三角形对应边成比例，对应角相等）。
∵$AD$，$BE$是$\triangle ABC$的高，$A'D'$，$B'E'$是$\triangle A'B'C'$的高，
∴$\angle ADB=\angle A'D'B'=90^{\circ}$，$\angle BED=\angle B'E'D'=90^{\circ}$。
在$Rt\triangle ABD$和$Rt\triangle A'B'D'$中，$\angle B = \angle B'$，$\angle ADB=\angle A'D'B'$，
∴$Rt\triangle ABD\sim Rt\triangle A'B'D'$（两角分别相等的两个直角三角形相似）。
∴$\frac{AD}{A'D'}=\frac{AB}{A'B'}$（相似三角形对应边成比例）。
在$Rt\triangle BCE$和$Rt\triangle B'C'E'$中，$\angle C = \angle C'$（相似三角形对应角相等），$\angle BEC=\angle B'E'C'=90^{\circ}$，
∴$Rt\triangle BCE\sim Rt\triangle B'C'E'$（两角分别相等的两个直角三角形相似）。
∴$\frac{BE}{B'E'}=\frac{BC}{B'C'}$。
又
∵$\frac{AB}{A'B'}=\frac{BC}{B'C'}$，
∴$\frac{AD}{A'D'}=\frac{BE}{B'E'}$。

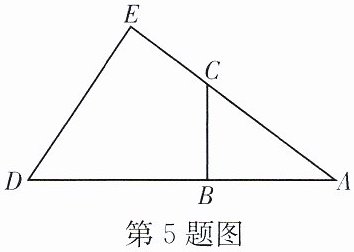
5. (24郴州期末)如图,点B,C分别在$\triangle ADE$的边AD,AE上.已知$\triangle ABC \backsim \triangle AED$,且$AC= 6$,$AB= 5$,$EC= 4$,求DB的长.

答案： 解：
∵AC=6，EC=4，
∴AE=AC+EC=6+4=10。
∵△ABC∽△AED，
∴$\frac{AB}{AE}=\frac{AC}{AD}$。
∵AB=5，AC=6，AE=10，
∴$\frac{5}{10}=\frac{6}{AD}$，
解得AD=12。
∵AB=5，
∴DB=AD-AB=12-5=7。
答：DB的长为7。

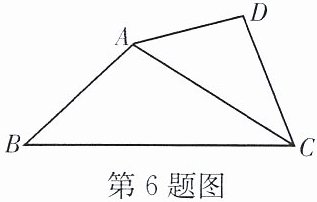
6. 如图,$AD= 2$,$AC= 4$,$BC= 6$,$\angle B= 36^\circ$,$\angle D= 107^\circ$,$\triangle ABC \backsim \triangle DAC$.
(1)求AB的长;
(2)求CD的长;
(3)求$\angle BAD$的大小.

答案：
(1)解：
∵△ABC∽△DAC，
∴$\frac{AB}{DA}=\frac{AC}{DC}=\frac{BC}{AC}$，
∴$\frac{AB}{AD}=\frac{BC}{AC}$，
∵AD=2，AC=4，BC=6，
∴$\frac{AB}{2}=\frac{6}{4}$，
解得AB=3。
(2)解：
∵△ABC∽△DAC，
∴$\frac{AC}{DC}=\frac{BC}{AC}$，
∴$\frac{4}{CD}=\frac{6}{4}$，
解得CD=$\frac{8}{3}$。
(3)解：
∵△ABC∽△DAC，
∴∠BAC=∠D，∠DAC=∠B，
∵∠B=36°，∠D=107°，
∴∠BAC=107°，∠DAC=36°，
∴∠BAD=∠BAC - ∠DAC=107° - 36°=71°。