2025年一本通武汉出版社九年级数学上册北师大版核心板
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年一本通武汉出版社九年级数学上册北师大版核心板 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 下列哪种光线形成的投影不是中心投影 ………………………………………………… (
A.探照灯
B.太阳
C.手电筒
D.路灯
B
)A.探照灯
B.太阳
C.手电筒
D.路灯
答案:
【解析】:
本题主要考察中心投影和平行投影的区别。中心投影是从一个点出发的所有光线经过物体后投射到某一平面上的投影,而平行投影是光线互相平行地投射到某一平面上的投影。
A选项:探照灯发出的光线可以看作是从一个点出发的,形成的是中心投影。
B选项:太阳距离地球非常远,其发出的光线在到达地球时可以近似看作是平行的,因此形成的是平行投影,不是中心投影。
C选项:手电筒发出的光线同样可以看作是从一个点(灯泡)出发的,形成的是中心投影。
D选项:路灯发出的光线也可以看作是从一个点出发的,形成的是中心投影。
综上所述,只有太阳形成的是平行投影,不是中心投影。
【答案】:
B
本题主要考察中心投影和平行投影的区别。中心投影是从一个点出发的所有光线经过物体后投射到某一平面上的投影,而平行投影是光线互相平行地投射到某一平面上的投影。
A选项:探照灯发出的光线可以看作是从一个点出发的,形成的是中心投影。
B选项:太阳距离地球非常远,其发出的光线在到达地球时可以近似看作是平行的,因此形成的是平行投影,不是中心投影。
C选项:手电筒发出的光线同样可以看作是从一个点(灯泡)出发的,形成的是中心投影。
D选项:路灯发出的光线也可以看作是从一个点出发的,形成的是中心投影。
综上所述,只有太阳形成的是平行投影,不是中心投影。
【答案】:
B
2. 广场上,一个大型字母宣传牌垂直于地面放置,其投影如图所示,则该投影属于
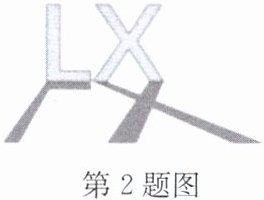
中心投影
.(填“平行投影”或“中心投影”)
答案:
【解析】:
本题考查投影的分类及判断。
投影分为中心投影和平行投影,其判断依据为:
如果是由同一点(点光源)发出的光线形成的投影叫做中心投影;
如果是由平行光线(如太阳光)形成的投影叫做平行投影。
观察题目中的投影图,可以看到字母宣传牌的投影呈现出从一点向外发散的形状,这是中心投影的典型特征,即投影线相交于一点。
因此,可以判断该投影属于中心投影。
【答案】:
中心投影
本题考查投影的分类及判断。
投影分为中心投影和平行投影,其判断依据为:
如果是由同一点(点光源)发出的光线形成的投影叫做中心投影;
如果是由平行光线(如太阳光)形成的投影叫做平行投影。
观察题目中的投影图,可以看到字母宣传牌的投影呈现出从一点向外发散的形状,这是中心投影的典型特征,即投影线相交于一点。
因此,可以判断该投影属于中心投影。
【答案】:
中心投影
3.(罗湖模拟)一幢4层楼房只有一个窗户亮着一盏灯,一棵小树和一根电线杆在窗口灯光下的影子如图所示,则亮着灯的窗口是

2
号窗口.
答案:
本题可通过中心投影的性质来确定亮着灯的窗口。
步骤一:明确中心投影的性质
中心投影是指把光由一点向外散射形成的投影。在中心投影中,连接物体和它影子的顶端所形成的直线必定经过点光源(即亮着灯的窗口)。
步骤二:根据中心投影性质确定亮着灯的窗口
分别连接小树的顶端与其影子的顶端、电线杆的顶端与其影子的顶端,得到两条直线,这两条直线的交点所在的窗口就是亮着灯的窗口。
通过观察图形,按照上述方法进行连线,可发现两条直线的交点在$2$号窗口处。
综上,亮着灯的窗口是$\boldsymbol{2}$号窗口。
步骤一:明确中心投影的性质
中心投影是指把光由一点向外散射形成的投影。在中心投影中,连接物体和它影子的顶端所形成的直线必定经过点光源(即亮着灯的窗口)。
步骤二:根据中心投影性质确定亮着灯的窗口
分别连接小树的顶端与其影子的顶端、电线杆的顶端与其影子的顶端,得到两条直线,这两条直线的交点所在的窗口就是亮着灯的窗口。
通过观察图形,按照上述方法进行连线,可发现两条直线的交点在$2$号窗口处。
综上,亮着灯的窗口是$\boldsymbol{2}$号窗口。
4. 如图,路灯下,广告标杆AB的影子是BC,小明(用线段DE表示)的影子是EF,在M处有一棵树,它的影子是MN.
(1)请在图中画出表示树高的线段(不写作法,保留作图痕迹);
(2)若已知点N,F到路灯的底部距离相等,小明身高为1.6 m,影长EF为1.8 m,树的影长MN是6 m,请计算树的高度.
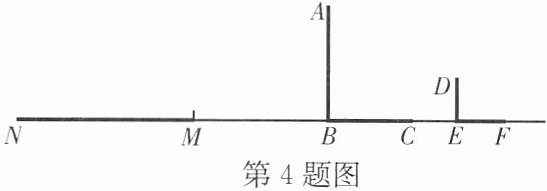
(1)请在图中画出表示树高的线段(不写作法,保留作图痕迹);
(2)若已知点N,F到路灯的底部距离相等,小明身高为1.6 m,影长EF为1.8 m,树的影长MN是6 m,请计算树的高度.

答案:
(1) (作图痕迹略,需连接路灯顶点与F、N,过M作垂线与光线交点即为树高顶点,线段为树高)
(2) 解:设路灯底部为点O,路灯高为h,树高为x。
由题意知ON=OF。
对于小明:$\frac{DE}{h}=\frac{EF}{OF}$,即$\frac{1.6}{h}=\frac{1.8}{OF}$。
对于树:$\frac{x}{h}=\frac{MN}{ON}$,因为ON=OF,MN=6m,所以$\frac{x}{h}=\frac{6}{OF}$。
两式相除得:$\frac{x}{1.6}=\frac{6}{1.8}$,解得$x=\frac{1.6×6}{1.8}=\frac{16}{3}\approx5.33$m。
答:树的高度为$\frac{16}{3}$m(或约5.33m)。
(1) (作图痕迹略,需连接路灯顶点与F、N,过M作垂线与光线交点即为树高顶点,线段为树高)
(2) 解:设路灯底部为点O,路灯高为h,树高为x。
由题意知ON=OF。
对于小明:$\frac{DE}{h}=\frac{EF}{OF}$,即$\frac{1.6}{h}=\frac{1.8}{OF}$。
对于树:$\frac{x}{h}=\frac{MN}{ON}$,因为ON=OF,MN=6m,所以$\frac{x}{h}=\frac{6}{OF}$。
两式相除得:$\frac{x}{1.6}=\frac{6}{1.8}$,解得$x=\frac{1.6×6}{1.8}=\frac{16}{3}\approx5.33$m。
答:树的高度为$\frac{16}{3}$m(或约5.33m)。
5.(24·凉山州)如图,一块面积为$60 cm^2$的三角形硬纸板(记为△ABC)平行于投影面时,在点光源O的照射下形成的投影是$△A_1B_1C_1,$若OB:$BB_1= 2$:3,则$△A_1B_1C_1$的面积是
375
$cm^2.$
答案:
解:
∵△ABC平行于投影面,点光源O照射形成投影△A₁B₁C₁,
∴△ABC∽△A₁B₁C₁。
∵OB:BB₁=2:3,
∴OB:OB₁=OB:(OB+BB₁)=2:(2+3)=2:5。
∵相似三角形面积比等于相似比的平方,
∴S△ABC:S△A₁B₁C₁=(OB:OB₁)²=4:25。
∵S△ABC=60cm²,
∴60:S△A₁B₁C₁=4:25,
解得S△A₁B₁C₁=375cm²。
∵△ABC平行于投影面,点光源O照射形成投影△A₁B₁C₁,
∴△ABC∽△A₁B₁C₁。
∵OB:BB₁=2:3,
∴OB:OB₁=OB:(OB+BB₁)=2:(2+3)=2:5。
∵相似三角形面积比等于相似比的平方,
∴S△ABC:S△A₁B₁C₁=(OB:OB₁)²=4:25。
∵S△ABC=60cm²,
∴60:S△A₁B₁C₁=4:25,
解得S△A₁B₁C₁=375cm²。
6. 如图,电灯P在横杆AB的正上方,AB在灯光下的影子为CD,AB//CD,AB= 1.5 m,CD= 4.5 m,点P到CD的距离为2.7 m,则AB与CD间的距离是
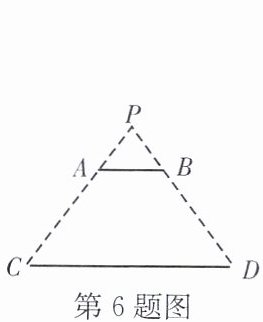
1.8
m.
答案:
解:设AB与CD间的距离为$x$ m,则点P到AB的距离为$(2.7 - x)$ m。
因为$AB// CD$,所以$\triangle PAB\sim\triangle PCD$。
根据相似三角形对应高的比等于相似比,可得:
$\frac{AB}{CD}=\frac{点P到AB的距离}{点P到CD的距离}$
即$\frac{1.5}{4.5}=\frac{2.7 - x}{2.7}$
解得$x = 1.8$
答:AB与CD间的距离是1.8 m。
因为$AB// CD$,所以$\triangle PAB\sim\triangle PCD$。
根据相似三角形对应高的比等于相似比,可得:
$\frac{AB}{CD}=\frac{点P到AB的距离}{点P到CD的距离}$
即$\frac{1.5}{4.5}=\frac{2.7 - x}{2.7}$
解得$x = 1.8$
答:AB与CD间的距离是1.8 m。
查看更多完整答案,请扫码查看


