《2025年一本通武汉出版社九年级数学上册北师大版核心板》

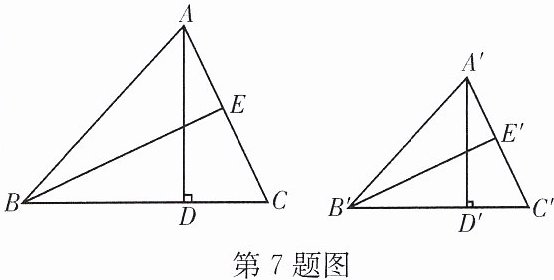
7. 如图,$\triangle ABC \backsim \triangle A'B'C'$,$AD,BE分别是\triangle ABC$的高和中线,$A'D',B'E'分别是\triangle A'B'C'$的高和中线,且$AD= 4$,$A'D'= 3$,$BE= 6$,则$B'E'$的长为 …………………… (D)

A.$\frac{3}{2}$
B.$\frac{5}{2}$
C.$\frac{7}{2}$
D.$\frac{9}{2}$

答案： 解：
∵△ABC∽△A'B'C'，AD、A'D'分别是对应高，
∴相似比k=AD/A'D'=4/3。
∵BE、B'E'分别是对应中线，
∴BE/B'E'=k=4/3。
∵BE=6，
∴6/B'E'=4/3，
解得B'E'=9/2。
答案：D

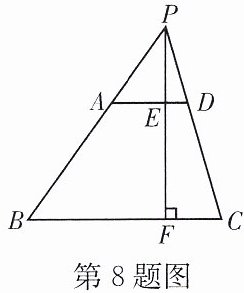
8. 如图,在四边形ABCD中,$AD // BC$,BA与CD的延长线相交于点P,$PF \perp BC$交AD于点E,$AD= 2$,$BC= 5$,$EF= 3$,求PF的长.

答案： 【解析】：本题考查相似三角形的性质，通过利用平行线构造相似三角形，再根据相似三角形的对应边成比例来求解$PF$的长。
因为$AD// BC$，$PF\perp BC$，所以$PF\perp AD$，则$\triangle PAE$和$\triangle PBF$相似。
根据相似三角形的性质，对应边成比例，可得到$\frac{PE}{PF}=\frac{AD}{BC}$，同时$PF = PE + EF$，通过设未知数建立方程求解$PF$。
【答案】：解：
∵$AD// BC$，$PF\perp BC$
∴$PF\perp AD$
设$PE = x$，则$PF=x + 3$
∵$\triangle PAE\sim\triangle PBF$
∴$\frac{PE}{PF}=\frac{AD}{BC}$
即$\frac{x}{x + 3}=\frac{2}{5}$
$5x = 2(x + 3)$
$5x = 2x + 6$
$3x = 6$
$x = 2$
∴$PF=x + 3 = 2 + 3 = 5$
答：$PF$的长为$5$。

9. 如图,在$Rt\triangle ABC$中,$\angle C= 90^\circ$,$BC= 4$,$AC= 8$,点D在斜边AB上,分别作$DE \perp AC$,$DF \perp BC$,垂足分别为点E,F,得四边形DECF,设$DE= x$,$DF= y$.
(1)用含y的代数式表示AE,得$AE= $$8 - y$;
(2)求y与x之间的函数关系式;$y=8 - 2x$
(3)设四边形DECF的面积为S,用含x代数式表示S:$8x - 2x^2$.

答案：
(1) 解：因为$AC=8$，四边形$DECF$是矩形（$DE\perp AC$，$DF\perp BC$，$\angle C=90^\circ$），所以$EC=DF=y$，则$AE=AC - EC=8 - y$。
(2) 解：因为$DE\perp AC$，$\angle C=90^\circ$，所以$DE// BC$，则$\triangle ADE\sim\triangle ABC$。所以$\frac{AE}{AC}=\frac{DE}{BC}$，即$\frac{8 - y}{8}=\frac{x}{4}$，解得$y=8 - 2x$。
(3) 解：四边形$DECF$的面积$S=DE× DF=x× y=x(8 - 2x)=8x - 2x^2$。
(1)$8 - y$
(2)$y=8 - 2x$
(3)$8x - 2x^2$

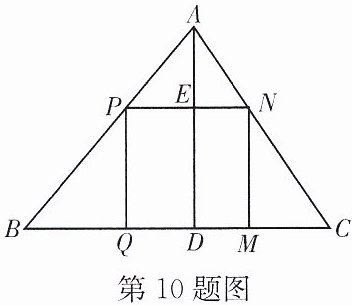
10. 如图,有一块三角形余料ABC,它的边$BC= 120\ \text{mm}$,高$AD= 80\ \text{mm}$.要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.问加工成的正方形零件的边长是多少?

答案： 解：设正方形零件的边长为 $ x \, \text{mm} $，正方形为 $ PQMN $，其中 $ PQ $、$ MN $ 在 $ BC $ 上，$ P $ 在 $ AB $ 上，$ N $ 在 $ AC $ 上，$ AD $ 交 $ PN $ 于 $ E $。
由正方形性质得 $ PN // BC $，$ PN = x $，$ AE = AD - ED = 80 - x $。
因为 $ PN // BC $，所以 $ \triangle APN \sim \triangle ABC $。
根据相似三角形性质：$\frac{PN}{BC} = \frac{AE}{AD}$，即$\frac{x}{120} = \frac{80 - x}{80}$。
解得：$80x = 120(80 - x)$
$80x = 9600 - 120x$
$200x = 9600$
$x = 48$。
答：加工成的正方形零件的边长是 $ 48 \, \text{mm} $。