2025年一本通武汉出版社九年级数学上册北师大版核心板
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年一本通武汉出版社九年级数学上册北师大版核心板 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
5. (24宁夏)如图,O是原点,菱形ABOC的顶点B在x轴上,点C(3,4),则点A的坐标是

(-2,4)
.
答案:
解:
∵点C(3,4),
∴OC的长度为$\sqrt{3^2 + 4^2} = 5$。
∵四边形ABOC是菱形,
∴AC=OC=5,且AC平行于OB。
∵点C的横坐标为3,AC=5且AC平行于x轴,
∴点A的横坐标为3 - 5 = -2,纵坐标与点C相同为4。
∴点A的坐标是(-2,4)。
答案:(-2,4)
∵点C(3,4),
∴OC的长度为$\sqrt{3^2 + 4^2} = 5$。
∵四边形ABOC是菱形,
∴AC=OC=5,且AC平行于OB。
∵点C的横坐标为3,AC=5且AC平行于x轴,
∴点A的横坐标为3 - 5 = -2,纵坐标与点C相同为4。
∴点A的坐标是(-2,4)。
答案:(-2,4)
6. (24绥化)如图,四边形ABCD是菱形,CD= 5,BD= 8,AE⊥BC于点E,则AE的长是______
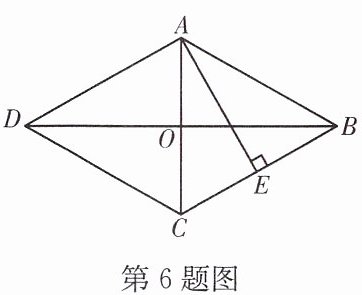
4.8
.
答案:
【解析】:本题考查菱形的性质。
根据菱形的对角线互相垂直且平分,可求出$AC$,$BO$的长度,进而求出$AB$,$BC$的长度,再根据菱形的面积等于底乘以高,也等于对角线乘积的一半,即可求出$AE$的长度。
因为四边形$ABCD$是菱形,$BD = 8$,
所以$AC\perp BD$,$DO=\frac{1}{2}BD = 4$,$BO=\frac{1}{2}BD = 4$,$AB = BC = CD = 5$。
在$Rt\triangle BOC$中,根据勾股定理$a^2+b^2=c^2$(其中$a$、$b$为直角边,$c$为斜边),可得:
$CO=\sqrt{BC^{2}-BO^{2}}=\sqrt{5^{2}-4^{2}}=\sqrt{25 - 16}=3$,
所以$AC = 2CO = 6$。
根据菱形面积公式$S=\frac{1}{2}× d_1× d_2$(其中$d_1$,$d_2$为菱形的两条对角线),可得:
$S_{菱形ABCD}=\frac{1}{2}× AC× BD=\frac{1}{2}×6×8 = 24$。
又因为$S_{菱形ABCD}=BC× AE$,即$5× AE = 24$,
所以$AE=\frac{24}{5}=4.8$。
【答案】:$4.8$。
根据菱形的对角线互相垂直且平分,可求出$AC$,$BO$的长度,进而求出$AB$,$BC$的长度,再根据菱形的面积等于底乘以高,也等于对角线乘积的一半,即可求出$AE$的长度。
因为四边形$ABCD$是菱形,$BD = 8$,
所以$AC\perp BD$,$DO=\frac{1}{2}BD = 4$,$BO=\frac{1}{2}BD = 4$,$AB = BC = CD = 5$。
在$Rt\triangle BOC$中,根据勾股定理$a^2+b^2=c^2$(其中$a$、$b$为直角边,$c$为斜边),可得:
$CO=\sqrt{BC^{2}-BO^{2}}=\sqrt{5^{2}-4^{2}}=\sqrt{25 - 16}=3$,
所以$AC = 2CO = 6$。
根据菱形面积公式$S=\frac{1}{2}× d_1× d_2$(其中$d_1$,$d_2$为菱形的两条对角线),可得:
$S_{菱形ABCD}=\frac{1}{2}× AC× BD=\frac{1}{2}×6×8 = 24$。
又因为$S_{菱形ABCD}=BC× AE$,即$5× AE = 24$,
所以$AE=\frac{24}{5}=4.8$。
【答案】:$4.8$。
7. (24海南)如图,菱形ABCD的周长为8,∠ABC= 120°,边AB在数轴上,将AC绕点A顺时针旋转,点C落在数轴上的点E处,若点E表示的数是3,则点A表示的数是______.
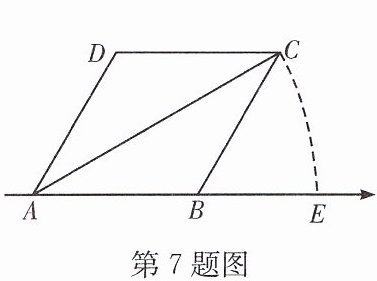

3 - 2√3
答案:
解:
∵菱形ABCD的周长为8,
∴AB=BC=CD=DA=2。
∵∠ABC=120°,
∴∠BAD=60°。
连接AC,在△ABC中,AB=BC=2,∠ABC=120°,
由余弦定理得AC²=AB²+BC²-2·AB·BC·cos∠ABC=2²+2²-2×2×2×cos120°=4+4-8×(-1/2)=12,
∴AC=2√3。
∵AC绕点A顺时针旋转后点C落在点E处,
∴AE=AC=2√3。
设点A表示的数为x,点E表示的数是3,且点E在点A右侧,
∴AE=3 - x=2√3,
∴x=3 - 2√3。
答案:3 - 2√3
∵菱形ABCD的周长为8,
∴AB=BC=CD=DA=2。
∵∠ABC=120°,
∴∠BAD=60°。
连接AC,在△ABC中,AB=BC=2,∠ABC=120°,
由余弦定理得AC²=AB²+BC²-2·AB·BC·cos∠ABC=2²+2²-2×2×2×cos120°=4+4-8×(-1/2)=12,
∴AC=2√3。
∵AC绕点A顺时针旋转后点C落在点E处,
∴AE=AC=2√3。
设点A表示的数为x,点E表示的数是3,且点E在点A右侧,
∴AE=3 - x=2√3,
∴x=3 - 2√3。
答案:3 - 2√3
8. 如图,AB//CD,直线MN交直线AB,CD于点M,N,MF平分∠BMN,NE平分∠CNM.
(1)求证:四边形ENFM为平行四边形;
(2)若四边形ENFM为菱形,求∠ENM的大小.
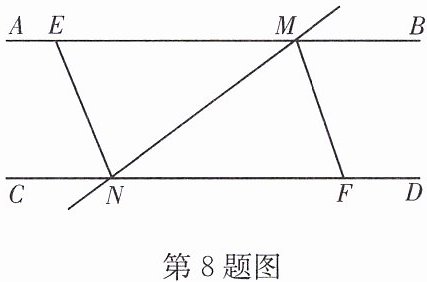
(1)求证:四边形ENFM为平行四边形;
(2)若四边形ENFM为菱形,求∠ENM的大小.

答案:
(1)证明:
∵AB//CD,
∴∠BMN=∠CNM。
∵MF平分∠BMN,NE平分∠CNM,
∴∠FMN=1/2∠BMN,∠ENM=1/2∠CNM,
∴∠FMN=∠ENM,
∴MF//NE。
∵AB//CD,即ME//NF,
∴四边形ENFM为平行四边形。
(2)解:
∵四边形ENFM为菱形,
∴ME=NE,
∴∠ENM=∠EMN。
由
(1)知∠FMN=∠ENM,∠BMN=∠CNM=2∠ENM。
设∠ENM=x,则∠EMN=x,∠BMN=2x。
∵AB为直线,∠EMN+∠BMN=180°,
即x+2x=180°,解得x=60°,
∴∠ENM=60°。
(1)证明:
∵AB//CD,
∴∠BMN=∠CNM。
∵MF平分∠BMN,NE平分∠CNM,
∴∠FMN=1/2∠BMN,∠ENM=1/2∠CNM,
∴∠FMN=∠ENM,
∴MF//NE。
∵AB//CD,即ME//NF,
∴四边形ENFM为平行四边形。
(2)解:
∵四边形ENFM为菱形,
∴ME=NE,
∴∠ENM=∠EMN。
由
(1)知∠FMN=∠ENM,∠BMN=∠CNM=2∠ENM。
设∠ENM=x,则∠EMN=x,∠BMN=2x。
∵AB为直线,∠EMN+∠BMN=180°,
即x+2x=180°,解得x=60°,
∴∠ENM=60°。
9. (24广东改编)如图,已知菱形ABCD的边长为2,∠ABC= 60°,点M,N分别是边BC,CD上的两个动点,∠MAN= 60°,连接MN.
(1)判别△AMN的形状,并说明理由.
(2)在点M,N运动的过程中,四边形CMAN的面积是否发生变化?若不变化,求出面积的值;若变化,说明理由.

(1)判别△AMN的形状,并说明理由.
(2)在点M,N运动的过程中,四边形CMAN的面积是否发生变化?若不变化,求出面积的值;若变化,说明理由.

答案:
【解析】:
(1)本题可根据菱形的性质、全等三角形的判定与性质以及等边三角形的判定来判别$\triangle AMN$的形状。
步骤一:连接$AC$,分析菱形的性质
已知四边形$ABCD$是菱形,$\angle ABC = 60^{\circ}$,因为菱形的四条边相等,且有一个角是$60^{\circ}$的菱形,其两条对角线将菱形分成四个直角三角形,其中包含$60^{\circ}$角的直角三角形是等边三角形的一半,所以可得$AB = BC = 2$,$\triangle ABC$是等边三角形,则$AB = AC$,$\angle BAC = 60^{\circ}$。
步骤二:证明$\triangle ABM\cong\triangle ACN$
因为$\angle BAC = \angle DAN = 60^{\circ}$,所以$\angle BAM+\angle MAC=\angle MAC+\angle CAN = 60^{\circ}$,根据等式的性质可得$\angle BAM = \angle CAN$。
又因为$\angle B = \angle ACD = 60^{\circ}$,$AB = AC$,根据“角边角”定理可得$\triangle ABM\cong\triangle ACN$。
步骤三:根据全等三角形的性质和等边三角形的判定得出$\triangle AMN$的形状
由$\triangle ABM\cong\triangle ACN$可得$AM = AN$,又因为$\angle MAN = 60^{\circ}$,根据有一个角是$60^{\circ}$的等腰三角形是等边三角形,所以$\triangle AMN$是等边三角形。
(2)本题可根据$\triangle ABM\cong\triangle ACN$得出四边形$CMAN$的面积与$\triangle ABC$面积的关系,进而判断四边形$CMAN$的面积是否发生变化。
步骤一:分析$\triangle ABM$与$\triangle ACN$全等的关系
因为$\triangle ABM\cong\triangle ACN$,根据全等三角形的面积相等,所以$S_{\triangle ABM}=S_{\triangle ACN}$。
步骤二:分析四边形$CMAN$的面积与$\triangle ABC$面积的关系
四边形$CMAN$的面积$S_{CMAN}=S_{\triangle AMC}+S_{\triangle ACN}$,将$S_{\triangle ACN}=S_{\triangle ABM}$代入可得$S_{CMAN}=S_{\triangle AMC}+S_{\triangle ABM}=S_{\triangle ABC}$。
步骤三:计算$\triangle ABC$的面积
已知$\triangle ABC$是边长为$2$的等边三角形,根据等边三角形面积公式$S = \frac{\sqrt{3}}{4}a^2$(其中$a$为等边三角形的边长),可得$S_{\triangle ABC}=\frac{\sqrt{3}}{4}×2^2=\sqrt{3}$,即四边形$CMAN$的面积不发生变化,其值为$\sqrt{3}$。
【答案】:
(1)$\triangle AMN$是等边三角形。理由如下:
连接$AC$,因为四边形$ABCD$是菱形,$\angle ABC = 60^{\circ}$,所以$AB = BC = 2$,$\triangle ABC$是等边三角形,则$AB = AC$,$\angle BAC = 60^{\circ}$。
因为$\angle BAM+\angle MAC=\angle MAC+\angle CAN = 60^{\circ}$,所以$\angle BAM = \angle CAN$。
又因为$\angle B = \angle ACD = 60^{\circ}$,$AB = AC$,所以$\triangle ABM\cong\triangle ACN(ASA)$,则$AM = AN$。
因为$\angle MAN = 60^{\circ}$,所以$\triangle AMN$是等边三角形。
(2)四边形$CMAN$的面积不发生变化。
因为$\triangle ABM\cong\triangle ACN$,所以$S_{\triangle ABM}=S_{\triangle ACN}$。
则$S_{CMAN}=S_{\triangle AMC}+S_{\triangle ACN}=S_{\triangle AMC}+S_{\triangle ABM}=S_{\triangle ABC}$。
因为$\triangle ABC$是边长为$2$的等边三角形,所以$S_{\triangle ABC}=\frac{\sqrt{3}}{4}×2^2=\sqrt{3}$,即四边形$CMAN$的面积为$\sqrt{3}$。
(1)本题可根据菱形的性质、全等三角形的判定与性质以及等边三角形的判定来判别$\triangle AMN$的形状。
步骤一:连接$AC$,分析菱形的性质
已知四边形$ABCD$是菱形,$\angle ABC = 60^{\circ}$,因为菱形的四条边相等,且有一个角是$60^{\circ}$的菱形,其两条对角线将菱形分成四个直角三角形,其中包含$60^{\circ}$角的直角三角形是等边三角形的一半,所以可得$AB = BC = 2$,$\triangle ABC$是等边三角形,则$AB = AC$,$\angle BAC = 60^{\circ}$。
步骤二:证明$\triangle ABM\cong\triangle ACN$
因为$\angle BAC = \angle DAN = 60^{\circ}$,所以$\angle BAM+\angle MAC=\angle MAC+\angle CAN = 60^{\circ}$,根据等式的性质可得$\angle BAM = \angle CAN$。
又因为$\angle B = \angle ACD = 60^{\circ}$,$AB = AC$,根据“角边角”定理可得$\triangle ABM\cong\triangle ACN$。
步骤三:根据全等三角形的性质和等边三角形的判定得出$\triangle AMN$的形状
由$\triangle ABM\cong\triangle ACN$可得$AM = AN$,又因为$\angle MAN = 60^{\circ}$,根据有一个角是$60^{\circ}$的等腰三角形是等边三角形,所以$\triangle AMN$是等边三角形。
(2)本题可根据$\triangle ABM\cong\triangle ACN$得出四边形$CMAN$的面积与$\triangle ABC$面积的关系,进而判断四边形$CMAN$的面积是否发生变化。
步骤一:分析$\triangle ABM$与$\triangle ACN$全等的关系
因为$\triangle ABM\cong\triangle ACN$,根据全等三角形的面积相等,所以$S_{\triangle ABM}=S_{\triangle ACN}$。
步骤二:分析四边形$CMAN$的面积与$\triangle ABC$面积的关系
四边形$CMAN$的面积$S_{CMAN}=S_{\triangle AMC}+S_{\triangle ACN}$,将$S_{\triangle ACN}=S_{\triangle ABM}$代入可得$S_{CMAN}=S_{\triangle AMC}+S_{\triangle ABM}=S_{\triangle ABC}$。
步骤三:计算$\triangle ABC$的面积
已知$\triangle ABC$是边长为$2$的等边三角形,根据等边三角形面积公式$S = \frac{\sqrt{3}}{4}a^2$(其中$a$为等边三角形的边长),可得$S_{\triangle ABC}=\frac{\sqrt{3}}{4}×2^2=\sqrt{3}$,即四边形$CMAN$的面积不发生变化,其值为$\sqrt{3}$。
【答案】:
(1)$\triangle AMN$是等边三角形。理由如下:
连接$AC$,因为四边形$ABCD$是菱形,$\angle ABC = 60^{\circ}$,所以$AB = BC = 2$,$\triangle ABC$是等边三角形,则$AB = AC$,$\angle BAC = 60^{\circ}$。
因为$\angle BAM+\angle MAC=\angle MAC+\angle CAN = 60^{\circ}$,所以$\angle BAM = \angle CAN$。
又因为$\angle B = \angle ACD = 60^{\circ}$,$AB = AC$,所以$\triangle ABM\cong\triangle ACN(ASA)$,则$AM = AN$。
因为$\angle MAN = 60^{\circ}$,所以$\triangle AMN$是等边三角形。
(2)四边形$CMAN$的面积不发生变化。
因为$\triangle ABM\cong\triangle ACN$,所以$S_{\triangle ABM}=S_{\triangle ACN}$。
则$S_{CMAN}=S_{\triangle AMC}+S_{\triangle ACN}=S_{\triangle AMC}+S_{\triangle ABM}=S_{\triangle ABC}$。
因为$\triangle ABC$是边长为$2$的等边三角形,所以$S_{\triangle ABC}=\frac{\sqrt{3}}{4}×2^2=\sqrt{3}$,即四边形$CMAN$的面积为$\sqrt{3}$。
查看更多完整答案,请扫码查看


