《2025年一本通武汉出版社九年级数学上册北师大版核心板》

6. 如图,在□ABCD中,点E为边CD上的一点,AE的延长线交BC的延长线于点F,请你写出图中的三对相似三角形: $\triangle ADE\sim\triangle FCE$, $\triangle ADE\sim\triangle FBA$, $\triangle FCE\sim\triangle FBA$.

答案： 【解析】：本题可根据平行四边形的性质以及相似三角形的判定定理来找出图中的相似三角形。
相似三角形的判定定理：两角分别相等的两个三角形相似。
在平行四边形$ABCD$中，$AD// BC$，$AB// CD$。
第一对相似三角形：$\triangle ADE$和$\triangle FCE$
因为$AD// BC$，即$AD// FC$，根据两直线平行，内错角相等，可得$\angle DAE = \angle F$，$\angle ADE = \angle FCE$。
在$\triangle ADE$和$\triangle FCE$中，有两个角分别相等，根据相似三角形的判定定理“两角分别相等的两个三角形相似”，所以$\triangle ADE\sim\triangle FCE$。
第二对相似三角形：$\triangle ADE$和$\triangle FBA$
由于$AB// CD$，即$AB// CE$，那么$\angle DAE = \angle F$（两直线平行，内错角相等），$\angle D = \angle ECF$（对顶角相等可转化为同位角相等），同时$\angle ADE=\angle FBA$（两直线平行，同位角相等）。
在$\triangle ADE$和$\triangle FBA$中，有两个角分别相等，根据相似三角形的判定定理“两角分别相等的两个三角形相似”，所以$\triangle ADE\sim\triangle FBA$。
第三对相似三角形：$\triangle FCE$和$\triangle FBA$
由前面可知$\angle F$为$\triangle FCE$和$\triangle FBA$的公共角，且$AB// CD$，所以$\angle FCE = \angle FBA$（两直线平行，同位角相等）。
在$\triangle FCE$和$\triangle FBA$中，有两个角分别相等，根据相似三角形的判定定理“两角分别相等的两个三角形相似”，所以$\triangle FCE\sim\triangle FBA$。
【答案】：$\triangle ADE\sim\triangle FCE$，$\triangle ADE\sim\triangle FBA$，$\triangle FCE\sim\triangle FBA$。

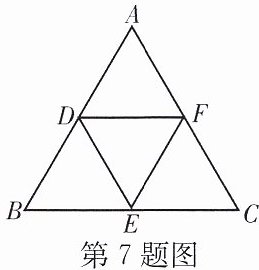
7. 如图,连接等边三角形ABC各边的中点D,E,F,得△DEF,△ABC的边长为4.
(1)△DEF与△ABC相似吗?如果相似,相似比是多少?
(2)分别求出△ABC和△DEF的面积.
(3)这两个三角形的面积比与边长之比有什么关系?

答案： 【解析】：本题主要考查相似三角形的判定、性质以及等边三角形面积的计算。
（1）判断$\triangle DEF$与$\triangle ABC$是否相似并求相似比：
相似三角形的判定定理：如果两个三角形的三组对应边的比相等，那么这两个三角形相似。
已知$D$、$E$、$F$分别是等边$\triangle ABC$各边的中点，根据三角形中位线定理：三角形的中位线平行于三角形的第三边，并且等于第三边的一半。
可得$DE=\frac{1}{2}AC$，$EF=\frac{1}{2}AB$，$DF=\frac{1}{2}BC$。
所以$\frac{DE}{AC}=\frac{EF}{AB}=\frac{DF}{BC}=\frac{1}{2}$。
因此，$\triangle DEF$与$\triangle ABC$相似，相似比是$1:2$。
（2）求$\triangle ABC$和$\triangle DEF$的面积：
等边三角形面积公式为$S = \frac{\sqrt{3}}{4}a^2$（$a$为边长）。
已知$\triangle ABC$的边长为$4$，将其代入公式可得：
$S_{\triangle ABC}=\frac{\sqrt{3}}{4}×4^2 = 4\sqrt{3}$。
因为$\triangle DEF$与$\triangle ABC$相似比为$1:2$，根据相似三角形面积比等于相似比的平方，可知$\triangle DEF$与$\triangle ABC$的面积比为$(1:2)^2 = 1:4$。
所以$S_{\triangle DEF}=\frac{1}{4}S_{\triangle ABC}=\frac{1}{4}×4\sqrt{3}=\sqrt{3}$。
（3）探究两个三角形的面积比与边长之比的关系：
由（2）可知$\triangle DEF$与$\triangle ABC$的边长之比为$1:2$，面积比为$1:4$，即面积比等于边长之比的平方。
【答案】：
(1)$\triangle DEF$与$\triangle ABC$相似，相似比是$1:2$；
(2)$S_{\triangle ABC}=4\sqrt{3}$，$S_{\triangle DEF}=\sqrt{3}$；
(3)这两个三角形的面积比等于边长之比的平方。

8.【回归课本】我们曾学习过一个基本事实:两条直线被一组平行线所截,所得的对应线段成比例.
【初步体验】(1)如图1,在△ABC中,点D在AB上,点E在AC上,DE//BC.若AD= 1,AE= 2,DB= 1.5,则EC=3,$\frac{AE}{AC}$=$\frac{2}{5}$;
(2)如图1,在△ABC中,点D,E分别在AB,AC上,且DE//BC.
求证:△ADE∽△ABC.
证明:过点E作AB的平行线交BC于点F.
$\because DE// BC$，$EF// AB$，
$\therefore$四边形$BDEF$是平行四边形，
$\therefore BD = EF$，$DE = BF$。
$\because EF// AB$，
$\therefore \angle A=\angle FEC$，$\angle B=\angle EFC$。
$\because \frac{AE}{EC}=\frac{AD}{DB}$，$BD = EF$，
$\therefore \frac{AE}{AC}=\frac{AD}{AB}$。
在$\triangle ADE$和$\triangle ABC$中，$\angle A=\angle A$，$\frac{AE}{AC}=\frac{AD}{AB}$，
$\therefore \triangle ADE\sim\triangle ABC$。
【深入探究】(3)如图2,如果一条直线与△ABC的三边AB,BC,CA或其延长线交于点D,F,E,那么$\frac{AE}{EC}\cdot\frac{BD}{DA}\cdot\frac{CF}{FB}$是否为定值?若是,试求出该定值;若不是,请说明理由.
是定值，定值为$1$。

答案： 【解析】：
(1)本题可根据平行线分线段成比例定理来求解$EC$的长度，再根据线段长度求出$\frac{AE}{AC}$的值。
因为$DE// BC$，根据平行线分线段成比例定理可得$\frac{AD}{DB}=\frac{AE}{EC}$。
已知$AD = 1$，$AE = 2$，$DB = 1.5$，将其代入$\frac{AD}{DB}=\frac{AE}{EC}$中，即$\frac{1}{1.5}=\frac{2}{EC}$，通过交叉相乘可得$EC = 2×1.5 = 3$。
$AC=AE + EC=2 + 3 = 5$，所以$\frac{AE}{AC}=\frac{2}{5}$。
故答案依次为$3$；$\frac{2}{5}$。
(2)本题可通过作辅助线，利用平行线的性质和平行线分线段成比例定理来证明$\triangle ADE\sim\triangle ABC$。
过点$E$作$EF// AB$交$BC$于点$F$，因为$DE// BC$，$EF// AB$，所以四边形$BDEF$是平行四边形，则$BD = EF$，$DE = BF$。
因为$EF// AB$，所以$\angle A=\angle FEC$，$\angle B=\angle EFC$（两直线平行，同位角相等）。
又因为$\frac{AE}{EC}=\frac{AD}{DB}$（平行线分线段成比例定理），且$BD = EF$，所以$\frac{AE}{AC}=\frac{AD}{AB}$。
在$\triangle ADE$和$\triangle ABC$中，$\angle A=\angle A$（公共角），$\frac{AE}{AC}=\frac{AD}{AB}$，根据相似三角形的判定定理“两边对应成比例且夹角相等的两个三角形相似”，可得$\triangle ADE\sim\triangle ABC$。
(3)本题需要分情况讨论直线与$\triangle ABC$三边或其延长线的交点情况，然后利用平行线分线段成比例定理来证明$\frac{AE}{EC}\cdot\frac{BD}{DA}\cdot\frac{CF}{FB}$为定值。
当点$D$，$F$，$E$分别在$AB$，$BC$，$CA$上时：
过点$A$作$AG// BC$交$DF$的延长线于点$G$。
因为$AG// BC$，所以$\triangle ADG\sim\triangle BDF$，则$\frac{BD}{DA}=\frac{BF}{AG}$；
又因为$AG// BC$，所以$\triangle AGE\sim\triangle CFE$，则$\frac{AE}{EC}=\frac{AG}{CF}$。
所以$\frac{AE}{EC}\cdot\frac{BD}{DA}\cdot\frac{CF}{FB}=\frac{AG}{CF}\cdot\frac{BF}{AG}\cdot\frac{CF}{FB}=1$。
当点$D$，$F$，$E$中有在边的延长线上时，同样可以通过作辅助线，利用相似三角形的性质和平行线分线段成比例定理得到$\frac{AE}{EC}\cdot\frac{BD}{DA}\cdot\frac{CF}{FB}=1$。
综上，$\frac{AE}{EC}\cdot\frac{BD}{DA}\cdot\frac{CF}{FB}$是定值，定值为$1$。
【答案】：
(1)$3$；$\frac{2}{5}$
(2)证明：过点$E$作$EF// AB$交$BC$于点$F$。
$\because DE// BC$，$EF// AB$，
$\therefore$四边形$BDEF$是平行四边形，
$\therefore BD = EF$，$DE = BF$。
$\because EF// AB$，
$\therefore \angle A=\angle FEC$，$\angle B=\angle EFC$。
$\because \frac{AE}{EC}=\frac{AD}{DB}$，$BD = EF$，
$\therefore \frac{AE}{AC}=\frac{AD}{AB}$。
在$\triangle ADE$和$\triangle ABC$中，$\angle A=\angle A$，$\frac{AE}{AC}=\frac{AD}{AB}$，
$\therefore \triangle ADE\sim\triangle ABC$。
(3)是定值，定值为$1$。