2025年一本通武汉出版社九年级数学上册北师大版核心板
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年一本通武汉出版社九年级数学上册北师大版核心板 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
6.(24西宁)如图,某小区在一个长60 m,宽22 m的矩形场地上,修建停车场,阴影部分为停车位所在区域,两侧是宽x m的道路,中间是宽2x m的道路. 如果阴影部分的总面积是$600 m^2,$那么x满足的方程是 ……………………………(
A
)
答案:
解:由题意得,矩形场地总面积为$60×22 = 1320 m^2$。
道路总面积为$1320 - 600 = 720 m^2$。
两侧道路面积为$2×60x = 120x m^2$,中间道路面积为$(22 - 2x)×2x = 44x - 4x^2 m^2$。
则$120x + 44x - 4x^2 = 720$,化简得$-4x^2 + 164x - 720 = 0$,两边同除以$-4$得$x^2 - 41x + 180 = 0$。
答案:A
道路总面积为$1320 - 600 = 720 m^2$。
两侧道路面积为$2×60x = 120x m^2$,中间道路面积为$(22 - 2x)×2x = 44x - 4x^2 m^2$。
则$120x + 44x - 4x^2 = 720$,化简得$-4x^2 + 164x - 720 = 0$,两边同除以$-4$得$x^2 - 41x + 180 = 0$。
答案:A
7.(24南通)红星村种的水稻2021年平均每公顷产7200 kg,2023年平均每公顷产8450 kg. 设水稻每公顷产量的年平均增长率为x,下列方程正确的是 ……………………………………(
$A. 7200(1+x)^2= 8450$
B. 7200(1+2x)= 8450
$C. 8450(1-x)^2= 7200$
D. 8450(1-2x)= 7200
A
)$A. 7200(1+x)^2= 8450$
B. 7200(1+2x)= 8450
$C. 8450(1-x)^2= 7200$
D. 8450(1-2x)= 7200
答案:
解:设水稻每公顷产量的年平均增长率为x,
2021年平均每公顷产7200kg,
2022年平均每公顷产7200(1+x)kg,
2023年平均每公顷产7200(1+x)(1+x)=7200(1+x)²kg,
已知2023年平均每公顷产8450kg,
则方程为7200(1+x)²=8450。
答案:A
2021年平均每公顷产7200kg,
2022年平均每公顷产7200(1+x)kg,
2023年平均每公顷产7200(1+x)(1+x)=7200(1+x)²kg,
已知2023年平均每公顷产8450kg,
则方程为7200(1+x)²=8450。
答案:A
8. 根据题意列出方程:
(1)两个数的积为12,和为7,设其中一个数为x,可列方程为
(2)直角三角形两条直角边的和为14 cm,面积为$24 cm^2,$设一条直角边长为x cm,可列方程为
(3)用22 cm长的铁丝折成一个面积为$30 cm^2$的矩形,设这个矩形的长为x cm,则宽为
(1)两个数的积为12,和为7,设其中一个数为x,可列方程为
x(7 - x) = 12
;(2)直角三角形两条直角边的和为14 cm,面积为$24 cm^2,$设一条直角边长为x cm,可列方程为
$\frac{1}{2}x(14 - x) = 24$
;(3)用22 cm长的铁丝折成一个面积为$30 cm^2$的矩形,设这个矩形的长为x cm,则宽为
(11 - x)cm
,可列方程为$x(11 - x) = 30$
.
答案:
(1)解:设其中一个数为$x$,则另一个数为$7 - x$,根据题意得$x(7 - x) = 12$
(2)解:设一条直角边长为$x$cm,则另一条直角边长为$(14 - x)$cm,根据题意得$\frac{1}{2}x(14 - x) = 24$
(3)解:设这个矩形的长为$x$cm,因为矩形周长为$22$cm,所以宽为$(11 - x)$cm,根据题意得$x(11 - x) = 30$
(1)解:设其中一个数为$x$,则另一个数为$7 - x$,根据题意得$x(7 - x) = 12$
(2)解:设一条直角边长为$x$cm,则另一条直角边长为$(14 - x)$cm,根据题意得$\frac{1}{2}x(14 - x) = 24$
(3)解:设这个矩形的长为$x$cm,因为矩形周长为$22$cm,所以宽为$(11 - x)$cm,根据题意得$x(11 - x) = 30$
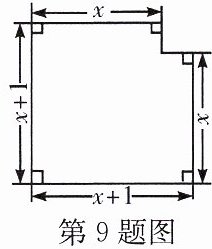
9. 已知如图所示的图形的面积为24,根据图中的条件,列出方程,并化成一般形式.

答案:
解:由图形可知,该图形为一个长为$x + 1$,宽为$x + 1$的大正方形减去一个边长为$1$的小正方形(右上角空缺部分)。
大正方形面积为$(x + 1)^2$,小正方形面积为$1^2 = 1$,已知图形面积为$24$,则可列方程:
$(x + 1)^2 - 1 = 24$
展开并化简:
$x^2 + 2x + 1 - 1 = 24$
$x^2 + 2x - 24 = 0$
一般形式为$x^2 + 2x - 24 = 0$
大正方形面积为$(x + 1)^2$,小正方形面积为$1^2 = 1$,已知图形面积为$24$,则可列方程:
$(x + 1)^2 - 1 = 24$
展开并化简:
$x^2 + 2x + 1 - 1 = 24$
$x^2 + 2x - 24 = 0$
一般形式为$x^2 + 2x - 24 = 0$
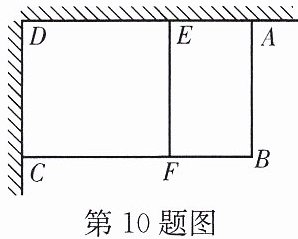
10. 如图,某单位在直角墙角处用可建60 m长围墙的建筑材料围成一个矩形堆物场地,中间用同样的材料分隔为两间,问AB为多长时,所围成的矩形堆物场地的面积是$450 m^2?$设AB的长为x m,列出方程,并化成一般形式.

答案:
解:设AB的长为x m,则BC的长为(60 - 2x)m。
根据题意,得x(60 - 2x) = 450。
化成一般形式为:2x² - 60x + 450 = 0。
根据题意,得x(60 - 2x) = 450。
化成一般形式为:2x² - 60x + 450 = 0。
11. 已知关于x的方程$(m^2-1)x^2-(m+1)x+m= 0.$
(1)m为何值时,此方程是一元一次方程?
(2)m为何值时,此方程是一元二次方程?并写出一元二次方程的二次项系数、一次项系数及常数项.
(1)m为何值时,此方程是一元一次方程?
(2)m为何值时,此方程是一元二次方程?并写出一元二次方程的二次项系数、一次项系数及常数项.
答案:
【解析】:
本题主要考察一元一次方程和一元二次方程的定义以及方程系数的识别。
(1) 要使方程$(m^2-1)x^2-(m+1)x+m= 0$成为一元一次方程,需要满足两个条件:
一是二次项系数$m^2 - 1 = 0$,
二是一次项系数$m + 1 \neq 0$。
解第一个方程$m^2 - 1 = 0$,得到$m = \pm 1$。
但由第二个条件$m + 1 \neq 0$,排除$m = -1$,所以只有$m = 1$满足条件。
(2) 要使方程$(m^2-1)x^2-(m+1)x+m= 0$成为一元二次方程,只需满足二次项系数$m^2 - 1 \neq 0$。
解这个不等式,得到$m \neq \pm 1$。
此时,一元二次方程的二次项系数为$m^2 - 1$,一次项系数为$-(m + 1)$,常数项为$m$。
【答案】:
(1) 当$m = 1$时,此方程是一元一次方程。
(2) 当$m \neq \pm 1$时,此方程是一元二次方程。
此时,二次项系数为$m^2 - 1$,一次项系数为$-(m + 1)$,常数项为$m$。
本题主要考察一元一次方程和一元二次方程的定义以及方程系数的识别。
(1) 要使方程$(m^2-1)x^2-(m+1)x+m= 0$成为一元一次方程,需要满足两个条件:
一是二次项系数$m^2 - 1 = 0$,
二是一次项系数$m + 1 \neq 0$。
解第一个方程$m^2 - 1 = 0$,得到$m = \pm 1$。
但由第二个条件$m + 1 \neq 0$,排除$m = -1$,所以只有$m = 1$满足条件。
(2) 要使方程$(m^2-1)x^2-(m+1)x+m= 0$成为一元二次方程,只需满足二次项系数$m^2 - 1 \neq 0$。
解这个不等式,得到$m \neq \pm 1$。
此时,一元二次方程的二次项系数为$m^2 - 1$,一次项系数为$-(m + 1)$,常数项为$m$。
【答案】:
(1) 当$m = 1$时,此方程是一元一次方程。
(2) 当$m \neq \pm 1$时,此方程是一元二次方程。
此时,二次项系数为$m^2 - 1$,一次项系数为$-(m + 1)$,常数项为$m$。
查看更多完整答案,请扫码查看


