《2025年一本通武汉出版社九年级数学上册北师大版核心板》

7. 如图,在$\triangle ABC$中,$DE// BC$,$EF// AB$. 若$AD= 2BD$,则$\frac{CF}{BF}= $$\frac{1}{2}$.

答案： 【解析】：本题可根据平行线分线段成比例定理来求解$\frac{CF}{BF}$的值。
已知$DE// BC$，$EF// AB$，$AD = 2BD$，即$\frac{AD}{BD}=2$。
根据平行线分线段成比例定理：三条平行线截两条直线，所得的对应线段成比例。
因为$DE// BC$，所以$\frac{AD}{BD}=\frac{AE}{EC}=2$，设$BD = x$，则$AD = 2x$，$AB=AD + BD=3x$。
又因为$EF// AB$，所以在$\triangle ABC$中，$\frac{CF}{BF}=\frac{CE}{AE}$。
由$\frac{AE}{EC}=2$，可得$\frac{CE}{AE}=\frac{1}{2}$，即$\frac{CF}{BF}=\frac{1}{2}$。
【答案】：$\frac{1}{2}$

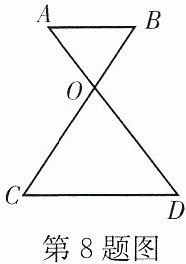
8. 如图,$AD与BC交于点O$,且$AB// CD$.
(1)已知$BO:BC= 1:3$,$CD= 6\space cm$,求$AB$的长；
(2)已知$BO:OC= 1:3$,$AD= 8\space cm$,求$OA$的长.

答案：
(1)解：
∵AB//CD，
∴△AOB∽△DOC，
∴$\frac{BO}{OC}=\frac{AB}{CD}$，
∵BO:BC=1:3，
∴BO:OC=1:2，
∵CD=6cm，
∴$\frac{1}{2}=\frac{AB}{6}$，
∴AB=3cm。
(2)解：
∵AB//CD，
∴△AOB∽△DOC，
∴$\frac{OA}{OD}=\frac{BO}{OC}$，
∵BO:OC=1:3，
∴$\frac{OA}{OD}=\frac{1}{3}$，
设OA=xcm，则OD=3xcm，
∵AD=OA+OD=8cm，
∴x+3x=8，
解得x=2，
∴OA=2cm。

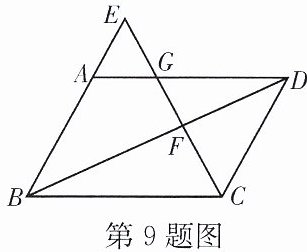
9. 如图,在$□ ABCD$中,$E是BA$延长线上一点,$CE与AD$,$BD交于点G$,$F$. 求证：$CF^{2}= GF\cdot EF$.

答案： 证明：
∵四边形ABCD是平行四边形，
∴AD//BC，AB//CD，AD=BC，AB=CD。
∵AD//BC，
∴△DFG∽△BFC，
∴$\frac{GF}{CF} = \frac{DF}{BF}$。
∵AB//CD，
∴△EFB∽△CFD，
∴$\frac{CF}{EF} = \frac{DF}{BF}$。
∴$\frac{GF}{CF} = \frac{CF}{EF}$，
∴$CF^2 = GF \cdot EF$。

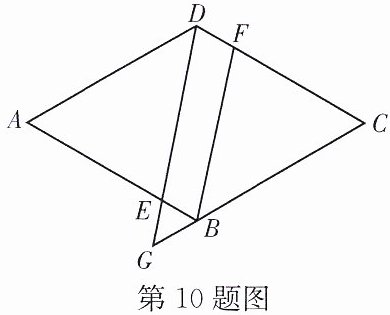
10. 如图,在菱形$ABCD$中,$BE= DF$,$DE和CB的延长线相交于点G$. 求证：(1)$\triangle ADE\cong\triangle CBF$；(2)$\frac{GE}{BF}= \frac{GB}{CD}$.

答案：
(1)证明：
∵四边形ABCD是菱形，
∴AD=BC，AD//BC，∠A=∠C，AB=CD，AB=AD，
∵BE=DF，AB=AD，
∴AB-BE=AD-DF，即AE=AF，
在△ADE和△CBF中，
$\left\{\begin{array}{l}AD=CB\\ \angle A=\angle C\\ AE=CF\end{array}\right.$，
∴△ADE≌△CBF(SAS)；
(2)证明：
∵四边形ABCD是菱形，
∴AD//BC，
∴△GED∽△GBC，
∴$\frac{GE}{GB}=\frac{DE}{BC}$，
∵△ADE≌△CBF，
∴DE=BF，
∵四边形ABCD是菱形，
∴BC=CD，
∴$\frac{GE}{GB}=\frac{BF}{CD}$，
∴$\frac{GE}{BF}=\frac{GB}{CD}$．