2025年一本通武汉出版社九年级数学上册北师大版核心板
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年一本通武汉出版社九年级数学上册北师大版核心板 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
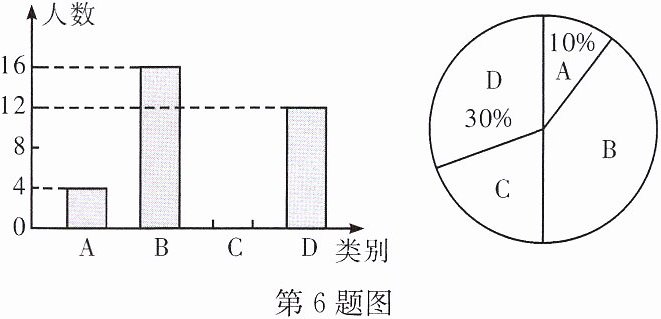
6. (24 宜宾)某校为了提升学生的综合素养,在课外活动中开设了四个兴趣小组:A. 插花组;B. 跳绳组;C. 话剧组;D. 书法组. 为了解学生对每个兴趣小组的参与情况,随机抽取了部分学生进行调查,并将调查结果绘制成如图所示的不完整的统计图.
请结合图中信息,解答下列问题:
(1)本次共调查了
(2)话剧组所对应扇形的圆心角为
(3)书法组成绩最好的 4 名学生由 3 名男生和 1 名女生构成. 从中随机抽取 2 名参加比赛,请用列表或画树状图的方法,求刚好抽到 1 名男生与 1名女生的概率.
解:设3名男生分别为1,2,3,1名女生为4,列表如下:
| | 1 | 2 | 3 | 4 |
| --- | --- | --- | --- | --- |
| 1 | - | (1,2) | (1,3) | (1,4) |
| 2 | (2,1) | - | (2,3) | (2,4) |
| 3 | (3,1) | (3,2) | - | (3,4) |
| 4 | (4,1) | (4,2) | (4,3) | - |
共有12种等可能的结果,其中刚好抽到1名男生与1名女生的结果有6种,
所以刚好抽到1名男生与1名女生的概率为$\frac{6}{12}=\frac{1}{2}$。
请结合图中信息,解答下列问题:
(1)本次共调查了
40
名学生,并将条形统计图补充完整;
(2)话剧组所对应扇形的圆心角为
72
°;(3)书法组成绩最好的 4 名学生由 3 名男生和 1 名女生构成. 从中随机抽取 2 名参加比赛,请用列表或画树状图的方法,求刚好抽到 1 名男生与 1名女生的概率.
解:设3名男生分别为1,2,3,1名女生为4,列表如下:
| | 1 | 2 | 3 | 4 |
| --- | --- | --- | --- | --- |
| 1 | - | (1,2) | (1,3) | (1,4) |
| 2 | (2,1) | - | (2,3) | (2,4) |
| 3 | (3,1) | (3,2) | - | (3,4) |
| 4 | (4,1) | (4,2) | (4,3) | - |
共有12种等可能的结果,其中刚好抽到1名男生与1名女生的结果有6种,
所以刚好抽到1名男生与1名女生的概率为$\frac{6}{12}=\frac{1}{2}$。
答案:
【解析】:
(1)首先,可以根据A类学生所占的百分比和人数来计算总调查的学生数。
A类学生有4人,占总人数的$10\%$,
所以总人数为:$4÷10\%=40(人)$。
接着,可以计算出C类学生的人数,方法是总人数减去A、B、D三类学生的人数:
$40-4-16-12=8(人)$。
因此,需要将条形统计图补充完整,C类学生的人数应为8人。
本次共调查了40名学生。
(2)话剧组(C类)在扇形统计图中所对应的圆心角可以通过以下公式计算:
$圆心角 = 360^\circ × \frac{话剧组人数}{总人数}= 360^\circ × \frac{8}{40}=72^\circ$。
(3)为了找出刚好抽到1名男生和1名女生的概率,可以使用列表法来列出所有可能的组合,并找出满足条件的组合数量。
设3名男生分别为1,2,3,1名女生为4,
则所有可能的组合为:$(1,2),(1,3),(1,4),(2,1),(2,3),(2,4),(3,1),(3,2),(3,4),(4,1),(4,2),(4,3)$,共12种情况。
其中,刚好抽到1名男生和1名女生的组合有:$(1,4),(2,4),(3,4),(4,1),(4,2),(4,3)$,共6种情况。
所以,刚好抽到1名男生和1名女生的概率为:$P=\frac{满足条件的组合数}{所有可能的组合数}=\frac{6}{12}=\frac{1}{2}$。
【答案】:
(1) 40;图略(C类学生的人数为8人);
(2) 72°;
(3) $\frac{1}{2}$。
(1)首先,可以根据A类学生所占的百分比和人数来计算总调查的学生数。
A类学生有4人,占总人数的$10\%$,
所以总人数为:$4÷10\%=40(人)$。
接着,可以计算出C类学生的人数,方法是总人数减去A、B、D三类学生的人数:
$40-4-16-12=8(人)$。
因此,需要将条形统计图补充完整,C类学生的人数应为8人。
本次共调查了40名学生。
(2)话剧组(C类)在扇形统计图中所对应的圆心角可以通过以下公式计算:
$圆心角 = 360^\circ × \frac{话剧组人数}{总人数}= 360^\circ × \frac{8}{40}=72^\circ$。
(3)为了找出刚好抽到1名男生和1名女生的概率,可以使用列表法来列出所有可能的组合,并找出满足条件的组合数量。
设3名男生分别为1,2,3,1名女生为4,
则所有可能的组合为:$(1,2),(1,3),(1,4),(2,1),(2,3),(2,4),(3,1),(3,2),(3,4),(4,1),(4,2),(4,3)$,共12种情况。
其中,刚好抽到1名男生和1名女生的组合有:$(1,4),(2,4),(3,4),(4,1),(4,2),(4,3)$,共6种情况。
所以,刚好抽到1名男生和1名女生的概率为:$P=\frac{满足条件的组合数}{所有可能的组合数}=\frac{6}{12}=\frac{1}{2}$。
【答案】:
(1) 40;图略(C类学生的人数为8人);
(2) 72°;
(3) $\frac{1}{2}$。
7. 解方程:
(1)$3x(x+2)= 4(x-1)+7$;
(2)$4000(1-x)^2= 3240$.
(1)$3x(x+2)= 4(x-1)+7$;
(2)$4000(1-x)^2= 3240$.
答案:
(1)解:$3x(x + 2) = 4(x - 1) + 7$
$3x^2 + 6x = 4x - 4 + 7$
$3x^2 + 6x - 4x - 3 = 0$
$3x^2 + 2x - 3 = 0$
$a = 3$,$b = 2$,$c = -3$
$\Delta = b^2 - 4ac = 2^2 - 4×3×(-3) = 4 + 36 = 40$
$x = \frac{-b \pm \sqrt{\Delta}}{2a} = \frac{-2 \pm \sqrt{40}}{2×3} = \frac{-2 \pm 2\sqrt{10}}{6} = \frac{-1 \pm \sqrt{10}}{3}$
$x_1 = \frac{-1 + \sqrt{10}}{3}$,$x_2 = \frac{-1 - \sqrt{10}}{3}$
(2)解:$4000(1 - x)^2 = 3240$
$(1 - x)^2 = 3240÷4000 = 0.81$
$1 - x = ±0.9$
当$1 - x = 0.9$时,$x = 1 - 0.9 = 0.1$
当$1 - x = -0.9$时,$x = 1 + 0.9 = 1.9$
$x_1 = 0.1$,$x_2 = 1.9$
(1)解:$3x(x + 2) = 4(x - 1) + 7$
$3x^2 + 6x = 4x - 4 + 7$
$3x^2 + 6x - 4x - 3 = 0$
$3x^2 + 2x - 3 = 0$
$a = 3$,$b = 2$,$c = -3$
$\Delta = b^2 - 4ac = 2^2 - 4×3×(-3) = 4 + 36 = 40$
$x = \frac{-b \pm \sqrt{\Delta}}{2a} = \frac{-2 \pm \sqrt{40}}{2×3} = \frac{-2 \pm 2\sqrt{10}}{6} = \frac{-1 \pm \sqrt{10}}{3}$
$x_1 = \frac{-1 + \sqrt{10}}{3}$,$x_2 = \frac{-1 - \sqrt{10}}{3}$
(2)解:$4000(1 - x)^2 = 3240$
$(1 - x)^2 = 3240÷4000 = 0.81$
$1 - x = ±0.9$
当$1 - x = 0.9$时,$x = 1 - 0.9 = 0.1$
当$1 - x = -0.9$时,$x = 1 + 0.9 = 1.9$
$x_1 = 0.1$,$x_2 = 1.9$
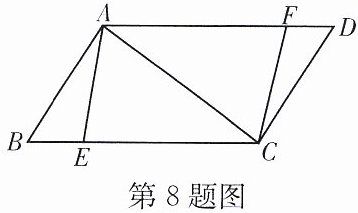
8. 如图,在□ABCD 中,$AB= 6$,$BC= 10$,对角线$AC⊥AB$,点 E,F 分别是边 BC,AD 上的点,且$BE= DF$.
(1)求证:四边形 AECF 是平行四边形.
(2)填空:①当 BE 的长度为
②当 BE 的长度为
(1)求证:四边形 AECF 是平行四边形.
(2)填空:①当 BE 的长度为
3.2
时,四边形 AECF 是菱形;②当 BE 的长度为
5
时,四边形 AECF 是矩形.
答案:
【解析】:
(1) 要证明四边形AECF是平行四边形,我们可以按照以下步骤进行:
首先,由于ABCD是平行四边形,根据平行四边形的性质,我们知道$AD// BC$且$AD = BC$。
然后,由于$DF = BE$,我们可以得出$AF = EC$(因为$AF = AD - DF$,$EC = BC - BE$,且$AD = BC$,$DF = BE$)。
接着,由于$AF// EC$(因为$AD// BC$),并且$AF = EC$,根据平行四边形的定义,我们可以得出四边形AECF是平行四边形。
(2)
① 要确定四边形AECF是菱形时BE的长度,我们可以按照以下步骤进行:
由于四边形AECF是菱形,根据菱形的性质,我们知道$AE = CE$。
又因为$AC\perp AB$,所以$\angle BAC = 90^\circ$。
在直角三角形ABC中,利用勾股定理,我们可以求出$AC = \sqrt{BC^2 - AB^2} = \sqrt{10^2 - 6^2} = 8$。
设$BE = x$,则$AE = CE = 10 - x$。
在直角三角形ABE中,利用勾股定理,我们有$AB^2 + BE^2 = AE^2$,即$6^2 + x^2 = (10 - x)^2$。
解这个方程,我们得到$x = 3.2$。
所以当$BE = 3.2$时,四边形AECF是菱形。
② 要确定四边形AECF是矩形时BE的长度,我们可以按照以下步骤进行:
由于四边形AECF是矩形,根据矩形的性质,我们知道$\angle AEC = 90^\circ$。
又因为$AC\perp AB$,所以点E必然是BC的中点(因为矩形对角线相等且互相平分,而AC已经垂直于AB,所以AE必须垂直于EC,即E是BC的中点)。
所以$BE = \frac{BC}{2} = 5$。
所以当$BE = 5$时,四边形AECF是矩形。
【答案】:
(1) 证明过程如上所述,四边形AECF是平行四边形。
(2) ① $3.2$;② $5$。
(1) 要证明四边形AECF是平行四边形,我们可以按照以下步骤进行:
首先,由于ABCD是平行四边形,根据平行四边形的性质,我们知道$AD// BC$且$AD = BC$。
然后,由于$DF = BE$,我们可以得出$AF = EC$(因为$AF = AD - DF$,$EC = BC - BE$,且$AD = BC$,$DF = BE$)。
接着,由于$AF// EC$(因为$AD// BC$),并且$AF = EC$,根据平行四边形的定义,我们可以得出四边形AECF是平行四边形。
(2)
① 要确定四边形AECF是菱形时BE的长度,我们可以按照以下步骤进行:
由于四边形AECF是菱形,根据菱形的性质,我们知道$AE = CE$。
又因为$AC\perp AB$,所以$\angle BAC = 90^\circ$。
在直角三角形ABC中,利用勾股定理,我们可以求出$AC = \sqrt{BC^2 - AB^2} = \sqrt{10^2 - 6^2} = 8$。
设$BE = x$,则$AE = CE = 10 - x$。
在直角三角形ABE中,利用勾股定理,我们有$AB^2 + BE^2 = AE^2$,即$6^2 + x^2 = (10 - x)^2$。
解这个方程,我们得到$x = 3.2$。
所以当$BE = 3.2$时,四边形AECF是菱形。
② 要确定四边形AECF是矩形时BE的长度,我们可以按照以下步骤进行:
由于四边形AECF是矩形,根据矩形的性质,我们知道$\angle AEC = 90^\circ$。
又因为$AC\perp AB$,所以点E必然是BC的中点(因为矩形对角线相等且互相平分,而AC已经垂直于AB,所以AE必须垂直于EC,即E是BC的中点)。
所以$BE = \frac{BC}{2} = 5$。
所以当$BE = 5$时,四边形AECF是矩形。
【答案】:
(1) 证明过程如上所述,四边形AECF是平行四边形。
(2) ① $3.2$;② $5$。
查看更多完整答案,请扫码查看


