《2025年一本通武汉出版社九年级数学上册北师大版核心板》

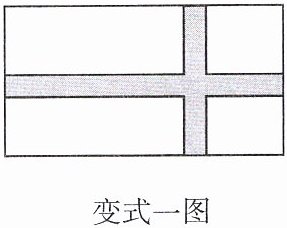
【变式一】如图,某农场有一块长40 m、宽32 m的矩形种植地,为方便管理,准备沿平行于两边的方向纵、横各修建一条等宽的小路,要使种植面积为$1140 m^2,$求小路的宽.
]

答案： 【解析】：本题可通过设未知数，根据矩形面积公式列出方程，进而求解小路的宽。
设小路的宽为$x$米。
由于小路是平行于矩形两边的，那么种植部分可看作一个新的矩形，其长为$(40 - x)$米，宽为$(32 - x)$米。
已知种植面积为$1140m^2$，根据矩形面积公式$S = 长×宽$，可列出方程$(40 - x)(32 - x) = 1140$。
接下来求解这个一元二次方程：
将方程$(40 - x)(32 - x) = 1140$展开可得：
$40×32-40x-32x+x^2=1140$
$1280 - 72x + x^2 = 1140$
移项化为一元二次方程的一般形式：
$x^2 - 72x + 1280 - 1140 = 0$
$x^2 - 72x + 140 = 0$
对于一元二次方程$ax^2 + bx + c = 0(a\neq0)$，这里$a = 1$，$b = -72$，$c = 140$，可使用求根公式$x=\frac{-b\pm\sqrt{b^2 - 4ac}}{2a}$求解，也可尝试因式分解。
对$x^2 - 72x + 140 = 0$进行因式分解得$(x - 2)(x - 70) = 0$。
则$x - 2 = 0$或$x - 70 = 0$，解得$x_1 = 2$，$x_2 = 70$。
因为矩形种植地的宽为$32$米，而$70\gt32$，小路的宽不可能超过矩形的宽，所以$x_2 = 70$不符合实际情况，应舍去。
因此，小路的宽为$2$米。
【答案】：小路的宽为$2m$。

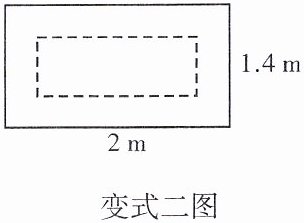
【变式二】如图,在一张矩形的床单四周绣上宽度相等的花边,剩下部分面积为$1.6 m^2.$已知床单的长是2 m,宽是1.4 m,求花边的宽度.
]

答案： 【解析】：本题考查一元二次方程的应用，关键在于根据矩形面积公式建立方程。
设花边的宽度为$x$米。
床单原来的长是$2$米，宽是$1.4$米，绣上花边后，剩下部分的长为$(2 - 2x)$米，宽为$(1.4 - 2x)$米。
已知剩下部分面积为$1.6m^2$，根据矩形面积公式$S = 长×宽$，可列出方程$(2 - 2x)(1.4 - 2x) = 1.6$。
展开括号得$2×1.4-2×2x-2x×1.4 + 4x^2 = 1.6$，即$2.8 - 4x - 2.8x + 4x^2 = 1.6$。
移项、合并同类项化为一元二次方程的一般形式为$4x^2 - 6.8x + 1.2 = 0$，两边同时除以$4$得$x^2 - 1.7x + 0.3 = 0$。
对于一元二次方程$ax^2 + bx + c = 0(a\neq0)$，这里$a = 1$，$b = -1.7$，$c = 0.3$，根据求根公式$x = \frac{-b\pm\sqrt{b^2 - 4ac}}{2a}$，可得$x = \frac{1.7\pm\sqrt{(-1.7)^2 - 4×1×0.3}}{2×1}=\frac{1.7\pm\sqrt{2.89 - 1.2}}{2}=\frac{1.7\pm\sqrt{1.69}}{2}=\frac{1.7\pm1.3}{2}$。
解得$x_1 = \frac{1.7 + 1.3}{2} = 1.5$，$x_2 = \frac{1.7 - 1.3}{2} = 0.2$。
因为$2x$表示两边花边的宽度和，$2x\lt2$且$2x\lt1.4$，即$x\lt1$且$x\lt0.7$，所以$x = 1.5$不符合实际情况，应舍去。
所以花边的宽度为$0.2$米。
【答案】：花边的宽度为$0.2m$。

【变式三】如图,利用一面墙,用80 m长的篱笆围成一个矩形场地.

(1)怎样围才能使矩形场地的面积为$750 m^2?$
(2)能否使所围的矩形场地面积为$810 m^2?$为什么?

答案： 解：（1）设矩形与墙垂直的边长为$x$ m，则与墙平行的边长为$(80 - 2x)$ m。
依题意，得$x(80 - 2x)=750$，
整理，得$x^2 - 40x + 375 = 0$，
解得$x_1 = 15$，$x_2 = 25$。
当$x = 15$时，$80 - 2x = 50$；
当$x = 25$时，$80 - 2x = 30$。
答：矩形的长为50 m、宽为15 m或长为30 m、宽为25 m时，面积为$750 m^2$。
（2）不能。
理由：设矩形与墙垂直的边长为$y$ m，则与墙平行的边长为$(80 - 2y)$ m。
依题意，得$y(80 - 2y)=810$，
整理，得$y^2 - 40y + 405 = 0$。
$\Delta=(-40)^2 - 4×1×405 = 1600 - 1620 = -20 ＜ 0$，
此方程无实数根，故不能使所围矩形场地面积为$810 m^2$。

【变式四】李明准备把一根长40 cm的铁丝剪成两段,并把每段首尾相连各围成一个正方形.
(1)要使这两个正方形的面积之和等于$58 cm^2,$李明应该怎么剪这根铁丝?
(2)李明认为这两个正方形的面积之和不可能等于$48 cm^2,$你认为他的说法正确吗?请说明理由.

答案：
(1)解：设其中一段铁丝长为$x$cm，则另一段长为$(40 - x)$cm。
第一个正方形边长为$\frac{x}{4}$cm，面积为$(\frac{x}{4})^2$cm²；第二个正方形边长为$\frac{40 - x}{4}$cm，面积为$(\frac{40 - x}{4})^2$cm²。
根据题意得：$(\frac{x}{4})^2 + (\frac{40 - x}{4})^2 = 58$
化简得：$\frac{x^2}{16} + \frac{(40 - x)^2}{16} = 58$
$x^2 + (40 - x)^2 = 58×16$
$x^2 + 1600 - 80x + x^2 = 928$
$2x^2 - 80x + 1600 - 928 = 0$
$2x^2 - 80x + 672 = 0$
$x^2 - 40x + 336 = 0$
$(x - 12)(x - 28) = 0$
解得$x_1 = 12$，$x_2 = 28$
当$x = 12$时，$40 - x = 28$；当$x = 28$时，$40 - x = 12$
答：李明应把铁丝剪成12cm和28cm的两段。
(2)解：李明的说法正确。理由如下：
假设两个正方形面积之和等于$48$cm²，依题意得：
$(\frac{x}{4})^2 + (\frac{40 - x}{4})^2 = 48$
化简得：$\frac{x^2}{16} + \frac{(40 - x)^2}{16} = 48$
$x^2 + (40 - x)^2 = 48×16$
$x^2 + 1600 - 80x + x^2 = 768$
$2x^2 - 80x + 1600 - 768 = 0$
$2x^2 - 80x + 832 = 0$
$x^2 - 40x + 416 = 0$
$\Delta = (-40)^2 - 4×1×416 = 1600 - 1664 = -64 ＜ 0$
此方程无实数根，故两个正方形面积之和不可能等于$48$cm²，李明的说法正确。