《2025年一本通武汉出版社九年级数学上册北师大版核心板》

9. 如图,若点A,B,C在同一直线上,且$AC:BC= 3:2$,则$AB:BC= $ …………………… (C)
A.$2:1$

B.$5:3$
C.$5:2$
D.$3:1$

答案： 【解析】：本题可根据线段的和差关系以及已知的比例关系来求解$AB:BC$的值。
已知点$A$，$B$，$C$在同一直线上，由图可知$AB = AC + BC$。
因为$AC:BC = 3:2$，设$AC = 3x$，$BC = 2x$（$x\neq0$）。
那么$AB=AC + BC=3x + 2x = 5x$。
所以$AB:BC = 5x:2x = 5:2$。
【答案】：C

10. 线段m,n,p,q的长度满足等式$mn= pq$,将它改成比例式的形式,错误的是 ………… (B)
A.$\frac{m}{p}= \frac{q}{n}$
B.$\frac{m}{n}= \frac{p}{q}$
C.$\frac{p}{m}= \frac{n}{q}$
D.$\frac{q}{m}= \frac{n}{p}$

答案： 【解析】：
本题主要考察比例式的变形和识别。
给定等式 $mn = pq$，需要将其改写成比例式的形式，并识别出哪个选项是错误的。
A选项：$\frac{m}{p} = \frac{q}{n}$，
交叉相乘得 $mn = pq$，与给定等式一致，所以A选项是正确的。
B选项：$\frac{m}{n} = \frac{p}{q}$，
交叉相乘得 $mq = pn$，这与给定等式 $mn = pq$ 不一致，所以B选项是错误的。
C选项：$\frac{p}{m} = \frac{n}{q}$，
交叉相乘得 $pq = mn$，与给定等式一致，所以C选项是正确的。
D选项：$\frac{q}{m} = \frac{n}{p}$，
交叉相乘得 $pq = mn$，与给定等式一致，所以D选项是正确的。
综上所述，错误的选项是B。
【答案】：
B

11. 如果$\frac{x+y}{3x}= \frac{1}{2}$,那么$\frac{y}{x}$的值为 ……………………………………………………… (A)
A.$\frac{1}{2}$
B.$\frac{2}{3}$
C.$\frac{1}{3}$
D.$\frac{2}{5}$

答案： 解：已知$\frac{x + y}{3x} = \frac{1}{2}$，
交叉相乘得：$2(x + y) = 3x$，
去括号：$2x + 2y = 3x$，
移项：$2y = 3x - 2x$，
合并同类项：$2y = x$，
两边同时除以$2x$（$x \neq 0$）：$\frac{y}{x} = \frac{1}{2}$。
答案：A

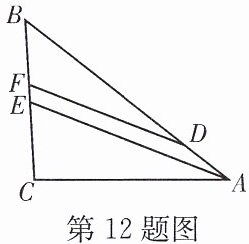
12. 如图,$\frac{AB}{AD}= \frac{BE}{EF}$,$AB= 10\ \text{cm}$,$AD= 2\ \text{cm}$,$BC= 7.2\ \text{cm}$,E是BC的中点,求EF,BF的长.

答案： 解：
∵E是BC的中点，BC=7.2cm
∴BE=BC/2=7.2/2=3.6cm
∵AB=10cm，AD=2cm
∴AB/AD=10/2=5
∵AB/AD=BE/EF
∴5=3.6/EF
∴EF=3.6/5=0.72cm
∵BF=BE+EF
∴BF=3.6+0.72=4.32cm
答：EF的长为0.72cm，BF的长为4.32cm。

$\boxed{\frac{a}{x}= \frac{y}{c}\xrightarrow{\text{当}x= y= b\text{时}}\frac{a}{b}= \frac{b}{c}\xrightarrow{\text{当}\frac{a}{c}= \text{2时}}\frac{a}{b}= \frac{b}{c}= \sqrt{2}}$

答案： 【解析】：本题考查比例中项及特殊线段比的知识点。
首先，我们根据题目给出的条件，有 $\frac{a}{b} = \frac{b}{c} = \sqrt{2}$。
根据比例中项的定义，如果 $\frac{a}{b} = \frac{b}{c}$，那么 $b$ 是 $a$ 和 $c$ 的比例中项，且满足 $b^2 = ac$。
由 $\frac{a}{b} = \sqrt{2}$，可得 $a = \sqrt{2}b$。
由 $\frac{b}{c} = \sqrt{2}$，可得 $c = \frac{b}{\sqrt{2}}$。
接下来，我们需要求出 $\frac{a}{c}$ 的值。
将 $a = \sqrt{2}b$ 和 $c = \frac{b}{\sqrt{2}}$ 代入 $\frac{a}{c}$，得到：
$\frac{a}{c} = \frac{\sqrt{2}b}{\frac{b}{\sqrt{2}}} = \sqrt{2} × \sqrt{2} = 2$。
【答案】：$2$。

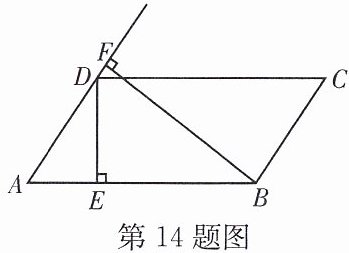
14. 如图,在$□ ABCD$中,$DE⊥AB$于点E,$BF⊥AD$交AD的延长线于点F.
(1)AB,BC,BF,DE这四条线段能否成比例? 如不能,请说明理由;如能,请写出比例式.
(2)若$AB= 10$,$DE= 2.5$,$BF= 5$,求BC的长.

答案： 【解析】：
(1)本题考查平行四边形的性质以及成比例线段的判定。
在平行四边形$ABCD$中，$AB // CD$，$AD // BC$，$AB = CD$，$AD = BC$。
已知$DE \perp AB$，$BF \perp AD$，根据平行四边形的面积公式$S = 底×高$，可得$S_{ABCD}=AB× DE = AD× BF$。
由$S_{ABCD}=AB× DE = AD× BF$，可得$\frac{AB}{AD}=\frac{BF}{DE}$，因为$AD = BC$，所以$\frac{AB}{BC}=\frac{BF}{DE}$，即$AB$，$BC$，$BF$，$DE$这四条线段能成比例，比例式为$\frac{AB}{BC}=\frac{BF}{DE}$。
(2)本题可根据上述比例式来计算$BC$的长。
由
(1)知$\frac{AB}{BC}=\frac{BF}{DE}$，已知$AB = 10$，$DE = 2.5$，$BF = 5$，将其代入比例式可得：
$\frac{10}{BC}=\frac{5}{2.5}$
交叉相乘可得：$5× BC = 10×2.5$，即$5BC = 25$，两边同时除以$5$，解得$BC = 5$。
【答案】：
(1)能成比例，比例式为$\frac{AB}{BC}=\frac{BF}{DE}$；
(2)$BC$的长为$5$。