2025年一本通武汉出版社九年级数学上册北师大版核心板
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年一本通武汉出版社九年级数学上册北师大版核心板 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1.(24北京)不透明袋子中仅有红、黄小球各一个,两个小球除颜色外无其他差别.从中随机摸出一个小球,放回并摇匀,再从中随机摸出一个小球,则两次摸出的都是红球的概率是···(
A.$\frac{1}{4}$
B.$\frac{1}{3}$
C.$\frac{1}{2}$
D.$\frac{3}{4}$
A
)A.$\frac{1}{4}$
B.$\frac{1}{3}$
C.$\frac{1}{2}$
D.$\frac{3}{4}$
答案:
解:列表如下:
|第一次/第二次|红|黄|
|----|----|----|
|红|(红,红)|(红,黄)|
|黄|(黄,红)|(黄,黄)|
共有4种等可能的结果,其中两次摸出的都是红球的结果有1种,所以两次摸出的都是红球的概率是$\frac{1}{4}$。
答案:A
|第一次/第二次|红|黄|
|----|----|----|
|红|(红,红)|(红,黄)|
|黄|(黄,红)|(黄,黄)|
共有4种等可能的结果,其中两次摸出的都是红球的结果有1种,所以两次摸出的都是红球的概率是$\frac{1}{4}$。
答案:A
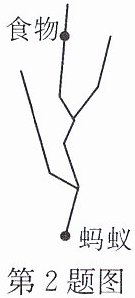
2.(24青海)如图,一只蚂蚁在树枝上寻觅食物,假定蚂蚁在每个叉路口都随机选择一条路径,它获得食物的概率是______.

1/3
答案:
解:蚂蚁从起点出发,第一个叉路口有2条路径可选,记为路径A和路径B。
若选择路径A,后续无叉路口,终点无食物;
若选择路径B,第二个叉路口有2条路径可选,记为路径B1和路径B2,其中路径B1终点有食物,路径B2终点无食物。
所有可能路径共2×1 + 1×2 = 4条(此处原解析有误,实际从图中可看出起点后第一个分叉有2条路,其中一条路直接到底无食物,另一条路又分2条路,一条有食物一条无,所以总路径数为1+2=3条,获得食物的路径1条)。
正确分析:总路径数为3条,获得食物的路径1条,所以概率为1/3。
答案:1/3
若选择路径A,后续无叉路口,终点无食物;
若选择路径B,第二个叉路口有2条路径可选,记为路径B1和路径B2,其中路径B1终点有食物,路径B2终点无食物。
所有可能路径共2×1 + 1×2 = 4条(此处原解析有误,实际从图中可看出起点后第一个分叉有2条路,其中一条路直接到底无食物,另一条路又分2条路,一条有食物一条无,所以总路径数为1+2=3条,获得食物的路径1条)。
正确分析:总路径数为3条,获得食物的路径1条,所以概率为1/3。
答案:1/3
3.算式:$1\triangle1\triangle1= □$,在每一个“△”中添加运算符号“+”或“-”后,通过计算,“□”中可得到不同的运算结果.求运算结果为1的概率.
答案:
解:在两个“△”中添加运算符号“+”或“-”,所有可能的情况如下:
1. “+,+”:$1+1+1=3$
2. “+,-”:$1+1-1=1$
3. “-,+”:$1-1+1=1$
4. “-,-”:$1-1-1=-1$
共有4种等可能的结果,其中运算结果为1的有2种。
所以运算结果为1的概率为$\frac{2}{4}=\frac{1}{2}$。
答:运算结果为1的概率为$\frac{1}{2}$。
1. “+,+”:$1+1+1=3$
2. “+,-”:$1+1-1=1$
3. “-,+”:$1-1+1=1$
4. “-,-”:$1-1-1=-1$
共有4种等可能的结果,其中运算结果为1的有2种。
所以运算结果为1的概率为$\frac{2}{4}=\frac{1}{2}$。
答:运算结果为1的概率为$\frac{1}{2}$。
4.小红上学要经过两个十字路口,每个路口遇到红、绿灯的机会都相同,小红希望上学时经过每个路口都是绿灯,但实际这样的概率是
$\frac{1}{4}$
.
答案:
【解析】:
本题考查的是概率的计算。
由于每个路口遇到红绿灯的机会都相同,所以每个路口遇到绿灯的概率是$\frac{1}{2}$。
因为小红要经过两个路口,并且希望每个路口都是绿灯,所以两个路口都是绿灯的概率是每个路口绿灯的概率的乘积。
即,$P(两个路口都是绿灯) = P(第一个路口是绿灯) × P(第二个路口是绿灯)$
$= \frac{1}{2} × \frac{1}{2}$
$= \frac{1}{4}$
【答案】:
$\frac{1}{4}$
本题考查的是概率的计算。
由于每个路口遇到红绿灯的机会都相同,所以每个路口遇到绿灯的概率是$\frac{1}{2}$。
因为小红要经过两个路口,并且希望每个路口都是绿灯,所以两个路口都是绿灯的概率是每个路口绿灯的概率的乘积。
即,$P(两个路口都是绿灯) = P(第一个路口是绿灯) × P(第二个路口是绿灯)$
$= \frac{1}{2} × \frac{1}{2}$
$= \frac{1}{4}$
【答案】:
$\frac{1}{4}$
5.(23甘孜州)一天晚上,小张帮助妈妈清洗两个只有颜色不同的有盖茶杯,突然停电了,小张只好把杯盖和茶杯随机搭配在一起.则颜色搭配正确的概率是______
$\frac{1}{2}$
.
答案:
解:设两个茶杯分别为A、B,对应的杯盖分别为a、b。
列表如下:
| 茶杯A搭配的杯盖 | 茶杯B搭配的杯盖 |
|------------------|------------------|
| a | b |
| b | a |
共有2种等可能的结果,其中颜色搭配正确的结果有1种(A-a,B-b)。
所以颜色搭配正确的概率是$\frac{1}{2}$。
答案:$\frac{1}{2}$
列表如下:
| 茶杯A搭配的杯盖 | 茶杯B搭配的杯盖 |
|------------------|------------------|
| a | b |
| b | a |
共有2种等可能的结果,其中颜色搭配正确的结果有1种(A-a,B-b)。
所以颜色搭配正确的概率是$\frac{1}{2}$。
答案:$\frac{1}{2}$
6.如图,一条直线上有两只蚂蚁,甲蚂蚁在点A处,乙蚂蚁在点B处,假定两只蚂蚁同时出发,爬行方向只能沿直线AB在“向左”或“向右”中随机选择,并且甲蚂蚁爬行的速度比乙蚂蚁快.
(1)甲蚂蚁选择“向左”爬行的概率为
(2)利用列表或画树状图的方法求两只蚂蚁开始爬行后会“触碰到”的概率.
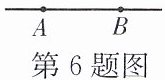
解:甲蚂蚁爬行方向:左、右;乙蚂蚁爬行方向:左、右。
列表如下:
| 甲 | 左 | 左 | 右 | 右 |
| --- | --- | --- | --- | --- |
| 乙 | 左 | 右 | 左 | 右 |
共有4种等可能结果,其中会“触碰到”的结果有2种(甲左乙右,甲右乙左)。
$P(\text{触碰到})=\frac{2}{4}=\frac{1}{2}$
(1)甲蚂蚁选择“向左”爬行的概率为
$\frac{1}{2}$
;(2)利用列表或画树状图的方法求两只蚂蚁开始爬行后会“触碰到”的概率.

解:甲蚂蚁爬行方向:左、右;乙蚂蚁爬行方向:左、右。
列表如下:
| 甲 | 左 | 左 | 右 | 右 |
| --- | --- | --- | --- | --- |
| 乙 | 左 | 右 | 左 | 右 |
共有4种等可能结果,其中会“触碰到”的结果有2种(甲左乙右,甲右乙左)。
$P(\text{触碰到})=\frac{2}{4}=\frac{1}{2}$
答案:
(1) $\frac{1}{2}$
(2) 解:甲蚂蚁爬行方向:左、右;乙蚂蚁爬行方向:左、右。
列表如下:
| 甲 | 左 | 左 | 右 | 右 |
| --- | --- | --- | --- | --- |
| 乙 | 左 | 右 | 左 | 右 |
共有4种等可能结果,其中会“触碰到”的结果有2种(甲左乙右,甲右乙左)。
$P(\text{触碰到})=\frac{2}{4}=\frac{1}{2}$
(1) $\frac{1}{2}$
(2) 解:甲蚂蚁爬行方向:左、右;乙蚂蚁爬行方向:左、右。
列表如下:
| 甲 | 左 | 左 | 右 | 右 |
| --- | --- | --- | --- | --- |
| 乙 | 左 | 右 | 左 | 右 |
共有4种等可能结果,其中会“触碰到”的结果有2种(甲左乙右,甲右乙左)。
$P(\text{触碰到})=\frac{2}{4}=\frac{1}{2}$
查看更多完整答案,请扫码查看


