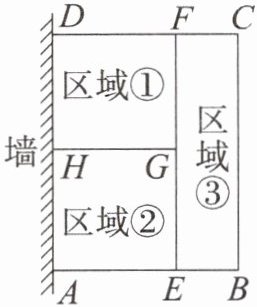
某花农计划在一面靠墙的空地(墙足够长)上种植花卉,他用总长为40m的篱笆围成了如图所示的矩形区域①②③.已知$AE= 2BE$,设BC的长度为x m,矩形区域ABCD的面积为$y m^{2}$.
(1)求BE的长(用含x的代数式表示);
(2)求y与x的函数解析式,并求矩形区域ABCD的面积的最大值.
(1)求BE的长(用含x的代数式表示);
(2)求y与x的函数解析式,并求矩形区域ABCD的面积的最大值.

答案:
(1)$(-\frac {1}{4}x+5)m$
(2)$y=-\frac {3}{4}x^{2}+15x$,矩形区域ABCD的面积的最大值为$75m^{2}$
(1)$(-\frac {1}{4}x+5)m$
(2)$y=-\frac {3}{4}x^{2}+15x$,矩形区域ABCD的面积的最大值为$75m^{2}$
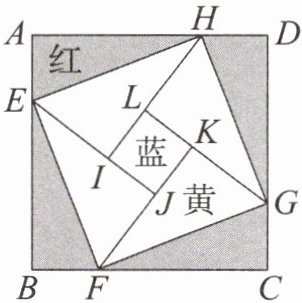
【问题背景】为了美化校园,某学校计划在如图所示的正方形ABCD花坛内种植红、蓝、黄三种颜色的花卉,在四个全等三角形(阴影部分)内种植红色花卉,正方形IJKL内种植蓝色花卉,剩下四个全等三角形内种植黄色花卉.已知AB的长为8m,$AE= LI$,红、蓝、黄三种花卉的单价分别为40元$/m^{2}$,100元$/m^{2}$,60元$/m^{2}$.
【建立模型】设AE的长为x m,购买花卉的总费用为W元.
(1)用含x的式子分别写出红、蓝、黄三种颜色花卉的种植面积;
(2)求W与x之间的函数解析式;
【方案决策】(3)当购买花卉的总费用最少时,求EI的长.
【建立模型】设AE的长为x m,购买花卉的总费用为W元.
(1)用含x的式子分别写出红、蓝、黄三种颜色花卉的种植面积;
(2)求W与x之间的函数解析式;
【方案决策】(3)当购买花卉的总费用最少时,求EI的长.

答案:
(1)红色:$(-2x^{2}+16x)m^{2}$;
蓝色:$x^{2}m^{2}$;黄色:$(x^{2}-16x+64)m^{2}$
(2)$W=80x^{2}-320x+3840$
(3)$(\sqrt {19}-1)m$
(1)红色:$(-2x^{2}+16x)m^{2}$;
蓝色:$x^{2}m^{2}$;黄色:$(x^{2}-16x+64)m^{2}$
(2)$W=80x^{2}-320x+3840$
(3)$(\sqrt {19}-1)m$
查看更多完整答案,请扫码查看


