1.【问题背景】如图 1,已知$\triangle ABC\backsim \triangle ADE$,求证:$\triangle ABD\backsim \triangle ACE$。
【尝试应用】如图 2,在$\triangle ABC和\triangle ADE$中,$\angle BAC= \angle DAE= 90^{\circ },\angle ABC= \angle ADE= 30^{\circ }$,$AC与DE相交于点F$,点$D在BC$边上,$\frac {AD}{BD}= \sqrt {3}$,求$\frac {DF}{CF}$的值。
【拓展创新】如图 3,$D是\triangle ABC$内一点,$\angle BAD= \angle CBD= 30^{\circ },\angle BDC= 90^{\circ },AB= 4,AC= 2\sqrt {3}$,直接写出$AD$的长。

【尝试应用】如图 2,在$\triangle ABC和\triangle ADE$中,$\angle BAC= \angle DAE= 90^{\circ },\angle ABC= \angle ADE= 30^{\circ }$,$AC与DE相交于点F$,点$D在BC$边上,$\frac {AD}{BD}= \sqrt {3}$,求$\frac {DF}{CF}$的值。
【拓展创新】如图 3,$D是\triangle ABC$内一点,$\angle BAD= \angle CBD= 30^{\circ },\angle BDC= 90^{\circ },AB= 4,AC= 2\sqrt {3}$,直接写出$AD$的长。

答案:
[问题背景]略
[尝试应用]3
[拓展创新]$AD=\sqrt {5}$
[尝试应用]3
[拓展创新]$AD=\sqrt {5}$
2. 如图 1,矩形$EBGF和矩形ABCD$共顶点,且绕着点$B$顺时针旋转,满足$\frac {BC}{AB}= \frac {BG}{BE}= \frac {3}{4}$。
(1)$\frac {DF}{AE}$的比值是否发生变化?若变化,说明理由;若不变,求出相应的值。
(2)在(1)的条件下,如图 2,若$F为CD$的中点,且$AB= 8,AD= 6$,连接$CG$,求$\triangle FCG$的
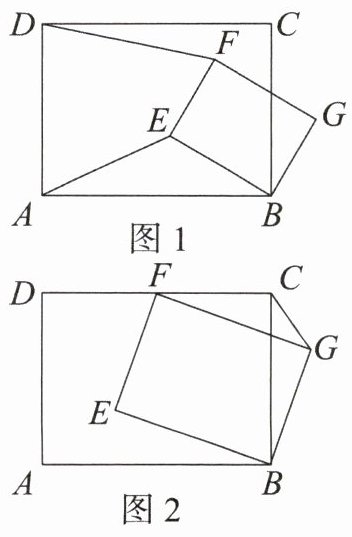
面积。
(1)$\frac {DF}{AE}$的比值是否发生变化?若变化,说明理由;若不变,求出相应的值。
(2)在(1)的条件下,如图 2,若$F为CD$的中点,且$AB= 8,AD= 6$,连接$CG$,求$\triangle FCG$的

面积。
答案:
(1)不发生变化,$\frac {DF}{AE}=\frac {5}{4}$
(2)$\frac {96}{25}$
(1)不发生变化,$\frac {DF}{AE}=\frac {5}{4}$
(2)$\frac {96}{25}$
查看更多完整答案,请扫码查看


