1. 如图,在$Rt△ABC$中,$∠ACB= 90^{\circ },CA= CB$,D 为 BC 上一点,$CE⊥AD$,垂足为 E,连接 BE,$∠BED= 45^{\circ }$。
(1) 求证:$CD^{2}= DE\cdot DA;$
(2) 求证:$CD= DB;$
(3) 求$\frac {AE}{BE}$的值。
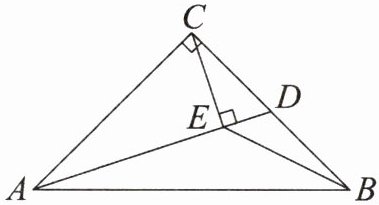
(1) 求证:$CD^{2}= DE\cdot DA;$
(2) 求证:$CD= DB;$
(3) 求$\frac {AE}{BE}$的值。

答案:
(1)略
(2)略
(3)$\sqrt{2}$
(1)略
(2)略
(3)$\sqrt{2}$
2. 如图,在$△ABC$中,P 为 AB 上一点。若 M 为 CP 的中点,$AC= 3,∠PBM= ∠ACP,AB= 5,$求 BP 的长。


答案:
4
3. 如图,在四边形 ABCD 中,$∠ADC= 90^{\circ },AC⊥BC,∠ABC= 45^{\circ }$,AC 与 BD 交于点 E。若$AB= 2\sqrt {10},CD= 2$,求$\frac {DE}{EB}$的值。


答案:
$\frac{2}{5}$
查看更多完整答案,请扫码查看


