二次函数与二倍角
方法 1 加倍
条件:$∠PBA= 2∠OAB$
方法:过点 A 作$AD// PB\Rightarrow ∠BAD= ∠PBA= 2∠OAB$
2. 如图,抛物线$y= \frac {1}{2}x^{2}-x-4$与 x 轴交于点 A,B,P 为第四象限内抛物线上一点,$C(-1,-\frac {5}{2})$为抛物线上一点,连接 PC,BC,若$∠PCB= 2∠CBO$,求点 P 的坐标.
方法 1:
方法 2 减半
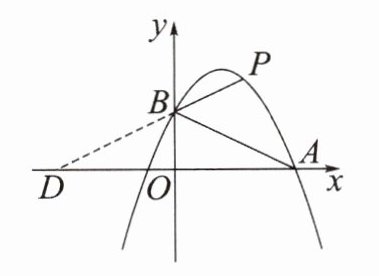
条件:$∠PBA= 2∠OAB$
方法:延长 PB 交 x 轴于点$D\Rightarrow ∠BDA= ∠BAD\Rightarrow OA= OD$
方法 2:
方法 3 减半
条件:$∠PBA= 2∠OAB$
方法:作$AD// y$轴,交 BP 的延长线于点 D,作$BH⊥AD于点H\Rightarrow ∠DBH= ∠ABH= ∠OAB\Rightarrow AD= 2OB$
方法 3:
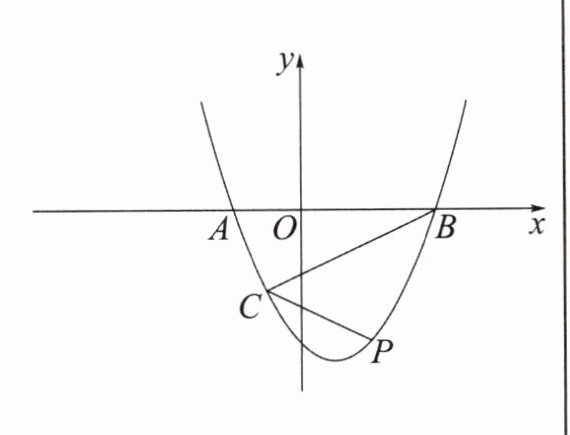
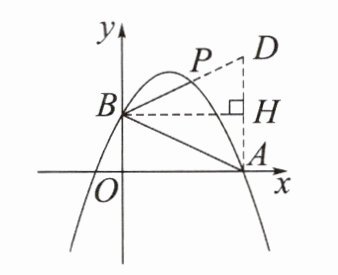
方法 1 加倍
条件:$∠PBA= 2∠OAB$
方法:过点 A 作$AD// PB\Rightarrow ∠BAD= ∠PBA= 2∠OAB$
2. 如图,抛物线$y= \frac {1}{2}x^{2}-x-4$与 x 轴交于点 A,B,P 为第四象限内抛物线上一点,$C(-1,-\frac {5}{2})$为抛物线上一点,连接 PC,BC,若$∠PCB= 2∠CBO$,求点 P 的坐标.
方法 1:
方法 2 减半

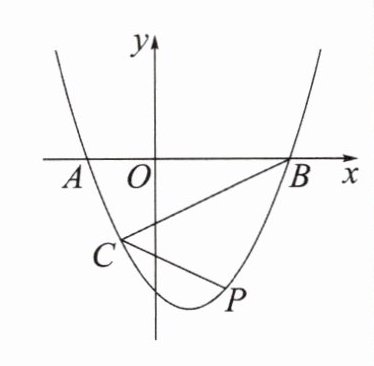
条件:$∠PBA= 2∠OAB$
方法:延长 PB 交 x 轴于点$D\Rightarrow ∠BDA= ∠BAD\Rightarrow OA= OD$
方法 2:
方法 3 减半
条件:$∠PBA= 2∠OAB$
方法:作$AD// y$轴,交 BP 的延长线于点 D,作$BH⊥AD于点H\Rightarrow ∠DBH= ∠ABH= ∠OAB\Rightarrow AD= 2OB$
方法 3:


答案:
$P(2,-4)$
特殊角
$45^{\circ }$角→构造等腰直角三角形→三垂直全等
条件:$∠PAB= 45^{\circ }$
方法:构造等腰直角三角形 ABQ,过点 Q 作$QH⊥y$轴,得$△ABO\cong △BQH$
3. 如图,在平面直角坐标系中,抛物线$y= x^{2}-2x-3$交 x 轴于$A(-1,0),B(3,0)$两点,交 y 轴于点 C. 若在 x 轴上方的抛物线上存在一点 D,使得$∠ACD= 45^{\circ }$,求点 D 的坐标.
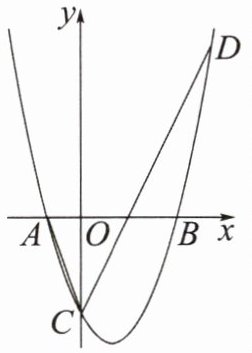
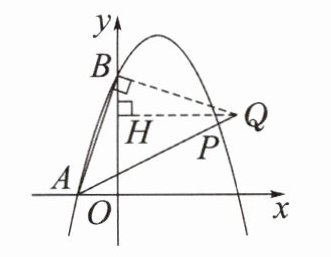
$45^{\circ }$角→构造等腰直角三角形→三垂直全等
条件:$∠PAB= 45^{\circ }$
方法:构造等腰直角三角形 ABQ,过点 Q 作$QH⊥y$轴,得$△ABO\cong △BQH$
3. 如图,在平面直角坐标系中,抛物线$y= x^{2}-2x-3$交 x 轴于$A(-1,0),B(3,0)$两点,交 y 轴于点 C. 若在 x 轴上方的抛物线上存在一点 D,使得$∠ACD= 45^{\circ }$,求点 D 的坐标.

答案:
$D(4,5)$
角的和差
$45^{\circ }$角的和差→构造全等三角形将角度转化
条件:$∠OBC= ∠OCB= 45^{\circ },∠DBC= 45^{\circ }-∠ACO$
方法:构造$△ACO\cong △HCO\Rightarrow ∠BCH= ∠OCB-∠HCO= 45^{\circ }-∠ACO= ∠D_{1}BC或构造△ACO\cong △EBO\Rightarrow ∠CBE= ∠CBO-∠EBO= 45^{\circ }-∠ACO= ∠D_{2}BC$
4. 如图,抛物线$y= ax^{2}+bx-3a(a≠0)$与 y 轴交于点$C(0,3)$,与 x 轴交于点 A 和点 B,点 A 在点 B 左侧,连接 AC,BC,对称轴为直线$x= 1.$
(1)求抛物线的函数解析式;
(2)若点 D 是抛物线上一动点,且满足$∠DBC= 45^{\circ }-∠ACO$,求点 D 的坐标.
$45^{\circ }$角的和差→构造全等三角形将角度转化
条件:$∠OBC= ∠OCB= 45^{\circ },∠DBC= 45^{\circ }-∠ACO$
方法:构造$△ACO\cong △HCO\Rightarrow ∠BCH= ∠OCB-∠HCO= 45^{\circ }-∠ACO= ∠D_{1}BC或构造△ACO\cong △EBO\Rightarrow ∠CBE= ∠CBO-∠EBO= 45^{\circ }-∠ACO= ∠D_{2}BC$
4. 如图,抛物线$y= ax^{2}+bx-3a(a≠0)$与 y 轴交于点$C(0,3)$,与 x 轴交于点 A 和点 B,点 A 在点 B 左侧,连接 AC,BC,对称轴为直线$x= 1.$
(1)求抛物线的函数解析式;
(2)若点 D 是抛物线上一动点,且满足$∠DBC= 45^{\circ }-∠ACO$,求点 D 的坐标.


答案:
(1) $ y = - x ^ { 2 } + 2 x + 3 $
(2) 点 $ D $ 的坐标为 $ (2,3) $ 或 $ \left( - \frac { 2 } { 3 }, \frac { 11 } { 9 } \right) $
(1) $ y = - x ^ { 2 } + 2 x + 3 $
(2) 点 $ D $ 的坐标为 $ (2,3) $ 或 $ \left( - \frac { 2 } { 3 }, \frac { 11 } { 9 } \right) $
角的和差
$90^{\circ }$角的和差→构造对称将角度转化
条件:$∠PCO-∠ACO= 90^{\circ }$
方法:构造点 A 的对称点$A'\Rightarrow ∠PCA'= 90^{\circ }$
5. 如图,抛物线$y= -\frac {2}{3}x^{2}+\frac {4}{3}x+2$与 x 轴交于 A,B 两点(点 A 在点 B 左侧),与 y 轴交于点 C,P 为抛物线上一点. 当$∠PCO-∠ACO= 90^{\circ }$时,求点 P 的坐标.
$90^{\circ }$角的和差→构造对称将角度转化
条件:$∠PCO-∠ACO= 90^{\circ }$
方法:构造点 A 的对称点$A'\Rightarrow ∠PCA'= 90^{\circ }$
5. 如图,抛物线$y= -\frac {2}{3}x^{2}+\frac {4}{3}x+2$与 x 轴交于 A,B 两点(点 A 在点 B 左侧),与 y 轴交于点 C,P 为抛物线上一点. 当$∠PCO-∠ACO= 90^{\circ }$时,求点 P 的坐标.
答案:
$P \left( \frac { 5 } { 4 }, \frac { 21 } { 8 } \right) $
查看更多完整答案,请扫码查看


