1. 如图,在$△ABC$中,$∠ACB= 90^{\circ }$,$∠B= 60^{\circ }$,$BC= 2$,若以$AC$为直径作半圆,交$AB边于点D$,点$O$为圆心,连接$OD$,则图中阴影部分的面积是____。
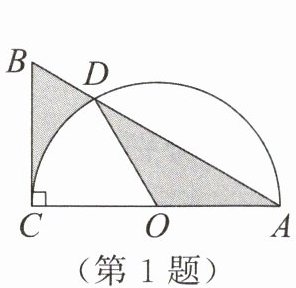

答案:
$ 2 \sqrt { 3 } - \frac { \pi } { 2 } $
2. 如图,在正方形$ABCD$中,点$O$为对角线的交点,以点$C$为圆心,以$OC$为半径作弧,交$BC于点F$,交$CD于点G$,以点$D$为圆心,以$AD$为半径作弧,交$BD于点E$。若$AB= 1$,则阴影部分的面积为____。
方法 2 构造和差法

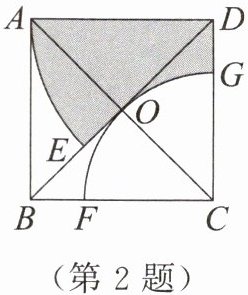
方法 2 构造和差法


答案:
$ \frac { 4 + \pi } { 16 } $
3. 如图,矩形$ABCD内接于\odot O$,$AD= 1$,$AC= 2$,则图中阴影部分的面积为()
A. $\frac {4π}{3}$
B. $\frac {1}{6}π+\frac {\sqrt {3}}{4}$
C. $\frac {1}{6}π+\frac {\sqrt {3}}{2}$
D. $\frac {3}{4}π+\frac {\sqrt {3}}{4}$
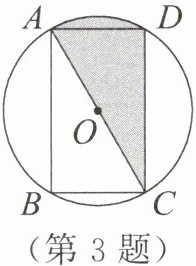
A. $\frac {4π}{3}$
B. $\frac {1}{6}π+\frac {\sqrt {3}}{4}$
C. $\frac {1}{6}π+\frac {\sqrt {3}}{2}$
D. $\frac {3}{4}π+\frac {\sqrt {3}}{4}$

答案:
B
4. 如图,在$Rt△ABC$中,$∠C= 90^{\circ }$,$∠A= 30^{\circ }$,$AB= 6$,若以点$C$为圆心,$CB$的长为半径画弧,交$AB于点D$,交$AC于点E$,则图中阴影部分的面积为____。
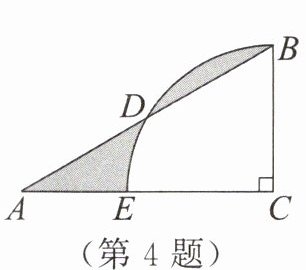

答案:
$ \frac { 3 } { 4 } \pi $
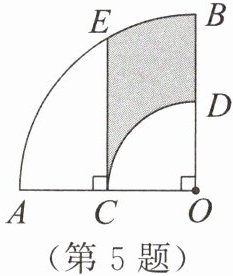
5. 如图,在扇形$AOB$中,$∠AOB= 90^{\circ }$,$C为OA$的中点,$CE⊥OA交弧AB于点E$,以点$O$为圆心,$OC的长为半径作弧CD交OB于点D$,若$OA= 4$,则阴影部分的面积为____。
方法 3 等积变换法
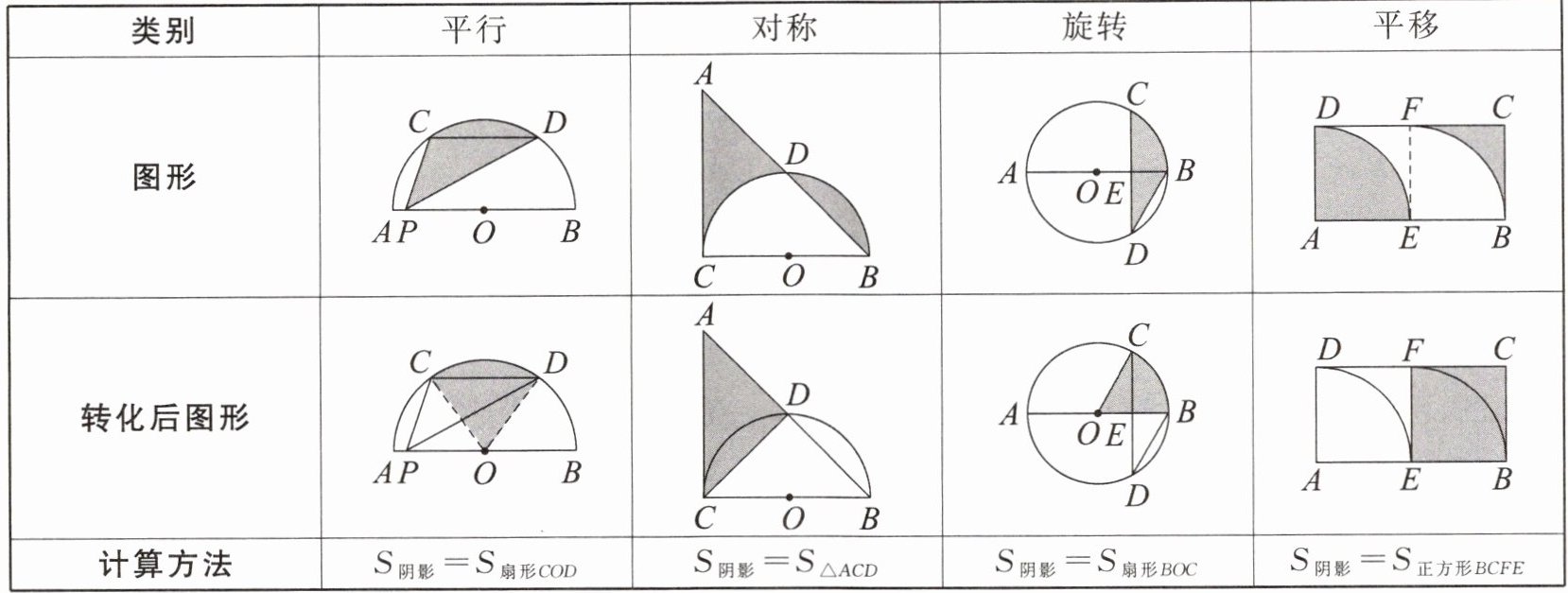
|类别|平行|对称|旋转|平移|
|----|----|----|----|----|
|图形|||||
|转化后图形|||||
|计算方法|$S_{阴影}= S_{扇形COD}$|$S_{阴影}= S_{△ACD}$|$S_{阴影}= S_{扇形BOC}$|$S_{阴影}= S_{正方形BCFE}$|
方法 3 等积变换法

|类别|平行|对称|旋转|平移|
|----|----|----|----|----|
|图形|||||
|转化后图形|||||
|计算方法|$S_{阴影}= S_{扇形COD}$|$S_{阴影}= S_{△ACD}$|$S_{阴影}= S_{扇形BOC}$|$S_{阴影}= S_{正方形BCFE}$|

答案:
$ \frac { \pi } { 3 } + 2 \sqrt { 3 } $
查看更多完整答案,请扫码查看


