《2025年阳光同学分层设计九年级数学全一册人教版福建专版》

例题精讲
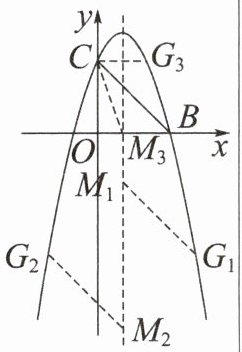
如图,抛物线$y= -x^{2}+2x+3$与 x 轴正半轴交于点 B,与 y 轴交于点 C。
(1)直接写出 B,C 两点的坐标和抛物线的对称轴。
(2)若 G 是抛物线上的一个动点,M 是抛物线对称轴上的一个动点,是否存在以 C,B,G,M 为顶点的四边形为平行四边形？若存在,求出点 G 的坐标；若不存在,请说明理由。
解：(1)B(3,0),C(0,3),对称轴为直线$x= 1$。
(2)存在。如图,设点$M(1,t),G(m,-m^{2}+2m+3)$。
根据点 M,G 所在位置设点坐标
①当 BC 为平行四边形的边时,有$|x_{M}-x_{G}|= x_{B}-x_{C}$,
分情况讨论 平移法
$\therefore |1-m|= 3-0.\therefore m= -2或4.\therefore G(-2,-5)或(4,-5)$。
②当 BC 为平行四边形的对角线时,有$\frac {x_{M}+x_{G}}{2}= \frac {x_{C}+x_{B}}{2}$,
分情况讨论 中点坐标公式
$\therefore 1+m= 0+3.\therefore m= 2.\therefore G(2,3)$。
综上所述,满足条件的点 G 的坐标为$(-2,-5)或(4,-5)或(2,3)$。

答案：
(1)$B(3,0)$，$C(0,3)$，对称轴为直线$x = 1$。
(2)存在，点$G$的坐标为$(-2,-5)$或$(4,-5)$或$(2,3)$。

1. 如图,抛物线$y= -x^{2}+3x+4$与 x 轴交于 A,B 两点(点 A 在点 B 的左侧),与 y 轴交于点 N,过点 A 的直线$l:y= -x-1$与 y 轴交于点 C,与抛物线$y= -x^{2}+3x+4$的另一个交点为 D,点 P 为抛物线$y= -x^{2}+3x+4$上一动点(不与点 A,D 重合)。设 M 为直线 l 上的点,探究是否存在点 M,使得以点 N,C,M,P 为顶点的四边形为平行四边形？若存在,求出点 M 的坐标；若不存在,请说明理由。

答案： 存在，点 M 的坐标为$(2+\sqrt {14},-3-\sqrt {14})$或$(2-\sqrt {14},-3+\sqrt {14})$或$(4,-5)$或$(-4,3)$