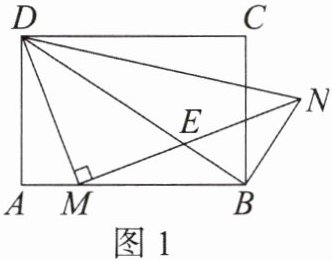
1. 在矩形 $ABCD$ 中,$AB = 6$,$AD = 4$,点 $M$ 为 $AB$ 边上一个动点,连接 $DM$,过点 $M$ 作 $MN \perp DM$,且 $MN = \frac{3}{2}DM$,连接 $DN$。
(1) 如图 1,连接 $BD$,$BN$,$BD$ 交 $MN$ 于点 $E$。
① 求证:$\triangle ABD \backsim \triangle MND$;
② 求证:$\angle CBN = \angle DNM$。
思路点拨:② 方法 1:结合 ① $\triangle ABD \backsim \triangle MND$ 得对应角 $\angle ABD = \angle DNM$,利用对顶角相等,寻找“蝴蝶”型 $\triangle MEB \backsim \triangle DEN$,进而寻找下一组“蝴蝶”型 $\triangle DME \backsim \triangle NBE$,从而得到 $\angle DBN = 90^{\circ}$,导角得到 $\angle CBN = \angle DNM$;
方法 2:结合 ① $\triangle ABD \backsim \triangle MND$ 得对应角 $\angle ABD = \angle DNM$,利用“四点共圆”,轻松得到 $\angle DBN = 90^{\circ}$。
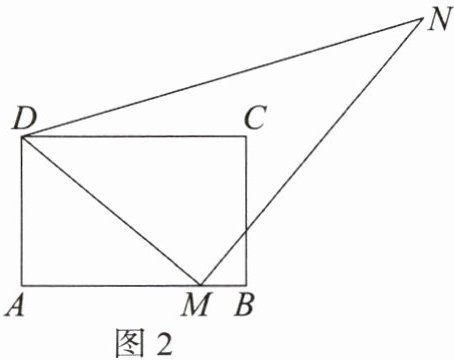
(2) 如图 2,当 $AM = 4BM$ 时,求证:$A$,$C$,$N$ 三点在同一条直线上。
思路点拨:根据 $\angle A = \angle DMN = 90^{\circ}$,作 $NF \perp AB$ 的延长线于点 $F$,构造“一线三垂直”型相似,根据 $AM = 4BM$,求出所有线段长度,判断 $\triangle ABC$ 和 $\triangle AFN$ 相似($A$ 字型相似),从而得到三点共线。
(1) 如图 1,连接 $BD$,$BN$,$BD$ 交 $MN$ 于点 $E$。
① 求证:$\triangle ABD \backsim \triangle MND$;
② 求证:$\angle CBN = \angle DNM$。
思路点拨:② 方法 1:结合 ① $\triangle ABD \backsim \triangle MND$ 得对应角 $\angle ABD = \angle DNM$,利用对顶角相等,寻找“蝴蝶”型 $\triangle MEB \backsim \triangle DEN$,进而寻找下一组“蝴蝶”型 $\triangle DME \backsim \triangle NBE$,从而得到 $\angle DBN = 90^{\circ}$,导角得到 $\angle CBN = \angle DNM$;
方法 2:结合 ① $\triangle ABD \backsim \triangle MND$ 得对应角 $\angle ABD = \angle DNM$,利用“四点共圆”,轻松得到 $\angle DBN = 90^{\circ}$。

(2) 如图 2,当 $AM = 4BM$ 时,求证:$A$,$C$,$N$ 三点在同一条直线上。
思路点拨:根据 $\angle A = \angle DMN = 90^{\circ}$,作 $NF \perp AB$ 的延长线于点 $F$,构造“一线三垂直”型相似,根据 $AM = 4BM$,求出所有线段长度,判断 $\triangle ABC$ 和 $\triangle AFN$ 相似($A$ 字型相似),从而得到三点共线。

答案:
(1)①略 ②略
(2)略
(1)①略 ②略
(2)略
查看更多完整答案,请扫码查看


