已知在四边形$ABCD$中,$AB = 8$,$E$,$F分别是AD$,$DC$边上的点,$BE\perp AF交于点G$。
(1)如图 1,若四边形$ABCD$是矩形,$BC = 10$,$BM平分\angle ABC交AD于点M$,交$AF于点H$。当$E为AM$的三等分点时,求$HM$的长;
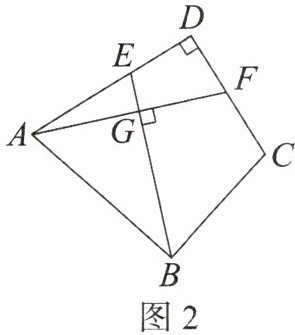
(2)如图 2,若$AD = AB$,$BC = CD = 6$,$\angle ADC = 90^{\circ}$,请直接写出$\frac{BE}{AF}$的值。
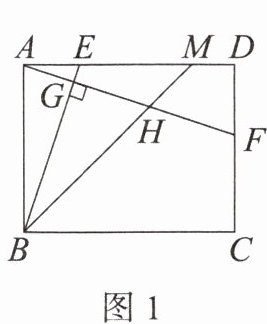
(1)如图 1,若四边形$ABCD$是矩形,$BC = 10$,$BM平分\angle ABC交AD于点M$,交$AF于点H$。当$E为AM$的三等分点时,求$HM$的长;
(2)如图 2,若$AD = AB$,$BC = CD = 6$,$\angle ADC = 90^{\circ}$,请直接写出$\frac{BE}{AF}$的值。


答案:
(1)$\frac {16\sqrt {2}}{5}$
(2)$\frac {BE}{AF}=\frac {24}{25}$
(1)$\frac {16\sqrt {2}}{5}$
(2)$\frac {BE}{AF}=\frac {24}{25}$
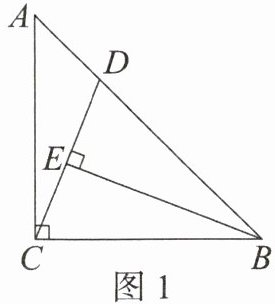
如图,在$\triangle ABC$中,$\angle ACB = 90^{\circ}$,$AC = CB$,$D为AB$边上一点,连接$CD$,过点$B作BE\perp CD$,交$CD于点E$。
(1)用等式表示$\angle ACE与\angle ABE$的数量关系,并说明理由;
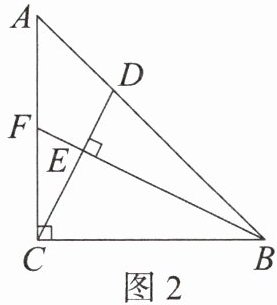
(2)如图 2,若$F为AC$的中点,连接$EF$,且$AD:DB = 1:2$,求证:$B$,$E$,$F$三点共线。
(1)用等式表示$\angle ACE与\angle ABE$的数量关系,并说明理由;
(2)如图 2,若$F为AC$的中点,连接$EF$,且$AD:DB = 1:2$,求证:$B$,$E$,$F$三点共线。


答案:
(1)$∠ABE+∠ACE=45^{\circ }$,理由略
(2)略
(1)$∠ABE+∠ACE=45^{\circ }$,理由略
(2)略
查看更多完整答案,请扫码查看


