2. 如图,抛物线$y= ax^{2}+bx-3$与 x 轴交于点$A(-3,0)和点B(1,0)$,与 y 轴交于点 C。
(1)求抛物线的解析式。
(2)点 E 为平面内一点,直线 AC 上方的对称轴上是否存在点 F,使得以 A,C,F,E 为顶点的四边形是菱形?若存在,请求出点 F 的坐标;若不存在,请说明理由。
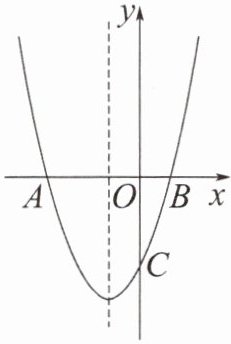
(1)求抛物线的解析式。
(2)点 E 为平面内一点,直线 AC 上方的对称轴上是否存在点 F,使得以 A,C,F,E 为顶点的四边形是菱形?若存在,请求出点 F 的坐标;若不存在,请说明理由。

答案:
(1)$y=x^{2}+2x-3$
(2)存在,点 F 的坐标为$(-1,-1)$或$(-1,\sqrt {17}-3)$或$(-1,\sqrt {14})$
(1)$y=x^{2}+2x-3$
(2)存在,点 F 的坐标为$(-1,-1)$或$(-1,\sqrt {17}-3)$或$(-1,\sqrt {14})$
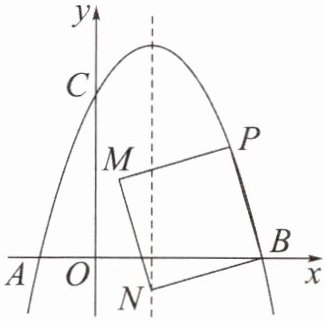
3. 如图,抛物线$y= -x^{2}+2x+3$与 x 轴交于 A,B 两点,与 y 轴交于点 C。P 为 x 轴上方抛物线上的一动点,以线段 PB 为一边,在直线$x= 3$左侧作正方形 BPMN,当点 M 或点 N 位于抛物线的对称轴上时,请求出点 P 的坐标。

答案:
点 P 的坐标为$(1-\sqrt {2},2)$或$(1+\sqrt {2},2)$或$(\frac {\sqrt {17}+1}{2},\frac {\sqrt {17}-1}{2})$
查看更多完整答案,请扫码查看


