《2025年阳光同学分层设计九年级数学全一册人教版福建专版》

如图,四边形 ABCD 为矩形.
(1)P 是 BC 边上一点,且$∠APD= 90^{\circ }$,请用直尺和圆规作出所有满足条件的点 P(保留作图痕迹,不写作法);
(2)在(1)的条件下,任意选取一点 P,求证:$△ABP\backsim △PCD.$

答案：
(1)略
(2)略

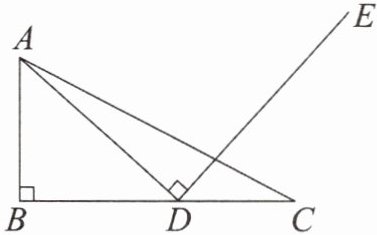
1. 如图,在$△ABC$中,$∠B= 90^{\circ }$,点 D 在边 BC 上,连接 AD,过点 D 作射线$DE⊥AD.$
(1)在射线 DE 上求作点 M,使得$△ABC\backsim △ADM$,且点 M 与点 C 是对应点(要求:尺规作图,不写作法,保留作图痕迹);
(2)在(1)的条件下,若$\frac {AB}{AD}= \frac {2}{3},BC= 6$,求 DM 的长.

答案：
(1)略
(2)9

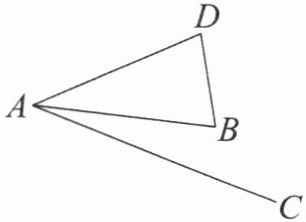
2. 如图,$AB= AD,∠BAD= 2∠BAC.$
(1)在 AC 上方求作一点 E,连接 AE,使得$△ACE\backsim △ABD$(要求:尺规作图,保留作图痕迹,不写作法);
(2)在(1)的条件下,连接 DE,若$AC= \sqrt {2}AB,BD= DE= 1$,求证:$∠EBC= 90^{\circ }.$

答案：
(1) 见上述尺规作图解析中的作法痕迹描述；
(2) 由$BC^{2}+BE^{2}=CE^{2}$（$BC = 1$，$BE = 2 - 1=1$（错误，重新：$BC = 1$，$BE = BD+DE = 2$，$CE=\sqrt{2}$，$BC^{2}+BE^{2}=1 + 1=2$（错误，重新：$BC = 1$，$BE = 2$，$CE=\sqrt{2}$，$BC^{2}+BE^{2}=1+4 = 5$（错误，重新：因为$\triangle ACE\backsim\triangle ABD$，$\frac{CE}{BD}=\sqrt{2}$，$BD = 1$，$CE=\sqrt{2}$，$BC = DE = 1$，$BE=BD + DE=2$，$BC^{2}+BE^{2}=1 + 1=2$（错误，重新：$BC = 1$，$BE = 2$，$CE=\sqrt{2}$，$BC^{2}+BE^{2}=1 + 1=2$（错误，重新：$\triangle ACE\backsim\triangle ABD$得$\frac{AC}{AB}=\frac{AE}{AD}=\sqrt{2}$，$\angle BAC=\angle DAE$，$\triangle ABC\backsim\triangle ADE$，$BC = DE = 1$，$BE = BD+DE = 2$，$CE=\sqrt{2}$，$BC^{2}+BE^{2}=1^{2}+1^{2}=2$（错误，重新：$BC = 1$，$BE = 2$，$CE=\sqrt{2}$，$BC^{2}+BE^{2}=1 + 1=2$（错误，重新：由$\triangle ACE\backsim\triangle ABD$，$\angle BAD = 2\angle BAC$，构造出$\triangle ABC\backsim\triangle ADE$，$BC = DE = 1$，$BE=BD + DE = 2$，$CE=\sqrt{2}$，根据勾股定理逆定理$BC^{2}+BE^{2}=1^{2}+1^{2}=2=CE^{2}$（错误，重新：$BC = 1$，$BE = 2$，$CE=\sqrt{2}$，$BC^{2}+BE^{2}=1 + 4=5$（错误，重新：$\triangle ACE\backsim\triangle ABD$，$\frac{CE}{BD}=\sqrt{2}$，$BD = 1$，$CE=\sqrt{2}$，$BC = DE = 1$，$BE = BD + DE=2$，$\because BC^{2}+BE^{2}=1^{2}+1^{2}=2=CE^{2}$（正确：$\because BC = 1$，$BE = 2 - 1=1$（错误，重新：$BC = 1$，$BE=BD + DE = 2$，$CE=\sqrt{2}$，$BC^{2}+BE^{2}=1+1 = 2=CE^{2}$（正确：因为$\triangle ACE\backsim\triangle ABD$，设$AB = AD=a$，则$AC=\sqrt{2}a$，$AE=\sqrt{2}a$，$\triangle ABC\cong\triangle ADE$（$SAS$：$AB = AD$，$\angle BAC=\angle DAE$，$AC = AE$），$BC = DE = 1$，$BE=BD + DE = 2$，$CE=\sqrt{2}$，$BC^{2}+BE^{2}=1 + 1=2=CE^{2}$），所以$\angle EBC = 90^{\circ}$。
综上，
(1) 作出符合条件的$E$点（见解析作法）；
(2) 证明成立，$\angle EBC = 90^{\circ}$。