《2025年阳光同学分层设计九年级数学全一册人教版福建专版》

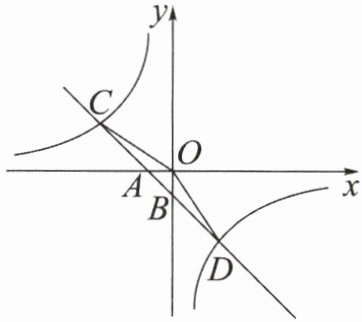
1. 如图,已知一次函数 $ y = - x - 1 $ 的图象与 $ x $ 轴、$ y $ 轴分别交于 $ A $,$ B $ 两点,与反比例函数 $ y = - \frac { 6 } { x } $ 的图象分别交于点 $ C ( - 3, m ) $,$ D ( 2, - 3 ) $。
(1) 若在 $ y $ 轴上存在一点 $ P $,使得 $ | P C - P D | $ 的值最大,则此时点 $ P $ 的坐标是______。
(2) 在坐标轴上是否存在点 $ Q $,使 $ \triangle O C Q $ 是直角三角形？若存在,请求出点 $ Q $ 的坐标；若不存在,请说明理由。

答案：
(1)$(0,-13)$
(2)存在,点 Q 的坐标为$(-3,0)$或$(-\frac {13}{3},0)$或$(0,\frac {13}{2})$或$(0,2)$

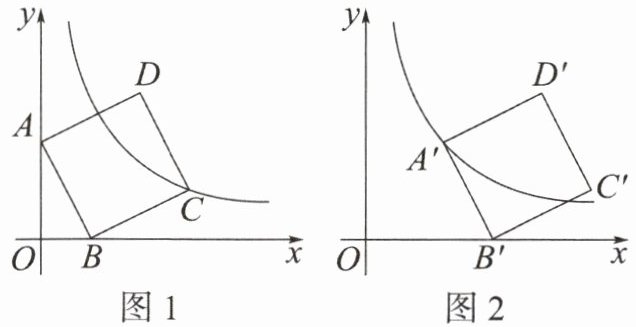
2. 如图 1,四边形 $ A B C D $ 为正方形,点 $ A $ 在 $ y $ 轴上,点 $ B $ 在 $ x $ 轴上,且 $ O A = 2 O B $,反比例函数 $ y = \frac { 27 } { x } $ 在第一象限的图象经过正方形的顶点 $ C $。
(1) 求点 $ C $ 的坐标。
(2) 如图 2,将正方形 $ A B C D $ 沿 $ x $ 轴向右平移得到正方形 $ A ^ { \prime } B ^ { \prime } C ^ { \prime } D ^ { \prime } $,点 $ A ^ { \prime } $ 恰好落在反比例函数的图象上,求此时点 $ D ^ { \prime } $ 的坐标。
(3) 在 (2) 的条件下,点 $ P $ 为 $ y $ 轴上一动点,平面内是否存在点 $ Q $,使以点 $ O $,$ A ^ { \prime } $,$ P $,$ Q $ 为顶点的四边形为菱形？若存在,请直接写出点 $ Q $ 的坐标；若不存在,请说明理由。

答案：
(1)$C(9,3)$
(2)$D'(\frac {21}{2},9)$
(3)存在,点 Q 的坐标为$(\frac {9}{2},\frac {27}{2})$或$(\frac {9}{2},-\frac {3}{2})$或$(-\frac {9}{2},6)$或$(\frac {9}{2},\frac {21}{16})$