《2025年阳光同学分层设计九年级数学全一册人教版福建专版》

4. 如图, 在 $ \text{Rt} \triangle ABC $ 中, $ \angle ACB = 90^{\circ} $, $ \angle B = 30^{\circ} $, $ AB = 4 $, $ P $ 是边 $ BC $ 上的一动点, 连接 $ AP $, 把线段 $ AP $ 绕点 $ A $ 顺时针旋转 $ 60^{\circ} $ 得到线段 $ AQ $, 连接 $ CQ $, 求线段 $ CQ $ 的最小值.

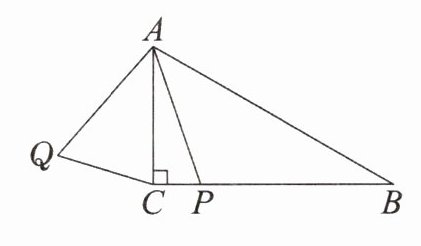
答案： 1

5. 如图, 在 $ \triangle ABC $ 中, $ AB = AC $, $ P $ 为 $ \triangle ABC $ 内的一点, $ \angle APB = \angle BAC = 120^{\circ} $, 若 $ AP + BP = 4 $, 求 $ PC $ 的最小值.

答案： $ 2 \sqrt { 3 } $

6. 如图, 在 $ \triangle ABC $ 中, $ AB = AC = 5 $, $ BC = 4\sqrt{5} $, 点 $ D $ 是边 $ AB $ 上一动点(点 $ B $ 除外), $ DC $ 绕点 $ D $ 逆时针旋转 $ 90^{\circ} $, 得到 $ DE $, 求 $ \triangle BDE $ 面积的最大值.

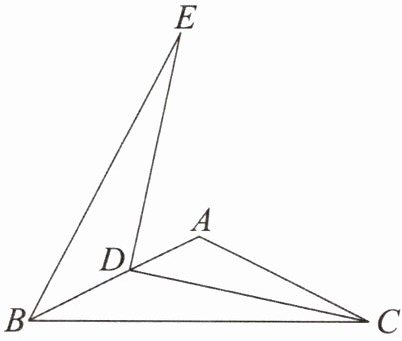
答案： 8