方法 1 三点定形法
满分技法:要证明的比例式的四条线段恰好是两个三角形的对应边时,可直接用“三点定形法”左右定形或上下定形找相似三角形.
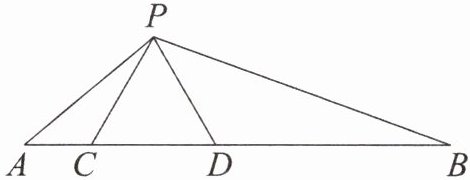
1. 如图,在$\triangle ABC$中,点$D$,$E分别在边AB$,$AC$上,$\angle AED= \angle B$,$AG平分\angle BAC$,分别交线段$DE$,$BC于点F$,$G$. 求证:$\frac{AD}{DF}= \frac{AC}{CG}$.
满分技法:要证明的比例式的四条线段恰好是两个三角形的对应边时,可直接用“三点定形法”左右定形或上下定形找相似三角形.
1. 如图,在$\triangle ABC$中,点$D$,$E分别在边AB$,$AC$上,$\angle AED= \angle B$,$AG平分\angle BAC$,分别交线段$DE$,$BC于点F$,$G$. 求证:$\frac{AD}{DF}= \frac{AC}{CG}$.
答案:
本题可先证明$\triangle ADE\sim\triangle ACB$,得出$\angle ADE = \angle C$,再结合$AG$平分$\angle BAC$证明$\triangle ADF\sim\triangle ACG$,最后根据相似三角形对应边成比例得到$\frac{AD}{DF}=\frac{AC}{CG}$。
方法 2 等线段代换法
满分技法:从要证的结论中难以找到相似三角形时,往往可用相等的线段去替换结论中的某些线段,再用“三点定形法”找相似三角形.
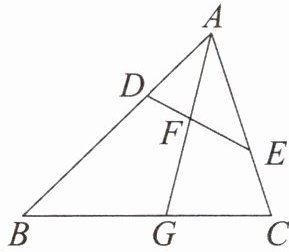
2. 代换一条线段 如图,在$\triangle ABC$中,点$D在边BC$上,$AD= AB$,点$E在边AC$上,且$\angle DEC= \angle ADB$. 求证:$AB^{2}= AE\cdot AC$.
\angle ADB$. 求证:$AB^{2}= AE\cdot AC$.
3. 代换两条线段 如图,点$C$,$D在线段AB$上,且$\triangle PCD$是等边三角形,$\angle APB= 120^{\circ}$. 求证:$CD^{2}= AC\cdot DB$.
满分技法:从要证的结论中难以找到相似三角形时,往往可用相等的线段去替换结论中的某些线段,再用“三点定形法”找相似三角形.
2. 代换一条线段 如图,在$\triangle ABC$中,点$D在边BC$上,$AD= AB$,点$E在边AC$上,且$\angle DEC=
 \angle ADB$. 求证:$AB^{2}= AE\cdot AC$.
\angle ADB$. 求证:$AB^{2}= AE\cdot AC$.3. 代换两条线段 如图,点$C$,$D在线段AB$上,且$\triangle PCD$是等边三角形,$\angle APB= 120^{\circ}$. 求证:$CD^{2}= AC\cdot DB$.


答案:
2. 证明过程如上述解析,证得$AB^{2}=AE\cdot AC$。
3. 证明过程如上述解析,证得$CD^{2}=AC\cdot DB$。
3. 证明过程如上述解析,证得$CD^{2}=AC\cdot DB$。
方法 3 等比例代换法
满分技法:要证明的比例式无法直接通过平行或相似得到时,往往要找中间比进行代换.
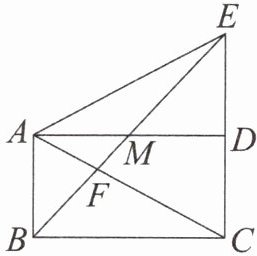
4. 如图,在矩形$ABCD$中,$M是边AD$上一点. 已知$AM= MD$,$BM交AC于点F$,$BM的延长线与CD的延长线交于点E$,连接$AE$. 求证:$\frac{MF}{BF}= \frac{EM}{EB}$.
满分技法:要证明的比例式无法直接通过平行或相似得到时,往往要找中间比进行代换.
4. 如图,在矩形$ABCD$中,$M是边AD$上一点. 已知$AM= MD$,$BM交AC于点F$,$BM的延长线与CD的延长线交于点E$,连接$AE$. 求证:$\frac{MF}{BF}= \frac{EM}{EB}$.

答案:
$\frac{MF}{BF}=\frac{EM}{EB}$得证。
查看更多完整答案,请扫码查看


