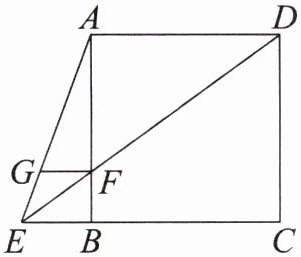
1. 如图,在正方形ABCD中,延长CB至点E,ED与AB相交于点F,过点F作$FG // BE$交AE于点G. 求证:$GF = FB$.

答案:
因为四边形$ABCD$是正方形,所以$AD// BC$,$AB// CD$,$AD = CD$。
由于$FG// BE$,$AB// CD$,则$FG// AD$。
所以$\triangle EFG\sim\triangle EDA$,可得$\frac{GF}{AD}=\frac{EF}{ED}$。
又因为$AB// CD$,所以$\triangle EFB\sim\triangle EDC$,则$\frac{FB}{CD}=\frac{EF}{ED}$。
因为$AD = CD$,所以$\frac{GF}{AD}=\frac{FB}{CD}$,进而得出$GF = FB$。
由于$FG// BE$,$AB// CD$,则$FG// AD$。
所以$\triangle EFG\sim\triangle EDA$,可得$\frac{GF}{AD}=\frac{EF}{ED}$。
又因为$AB// CD$,所以$\triangle EFB\sim\triangle EDC$,则$\frac{FB}{CD}=\frac{EF}{ED}$。
因为$AD = CD$,所以$\frac{GF}{AD}=\frac{FB}{CD}$,进而得出$GF = FB$。
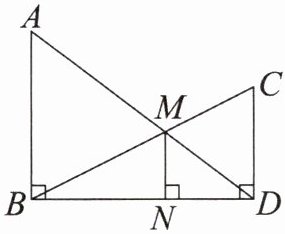
2. 如图,已知$BD \perp AB$,$BD \perp CD$,AD,BC交于点M,$MN \perp BD$. 若$AB = 12$,$CD = 8$,求MN的长.

答案:
$\frac{24}{5}$
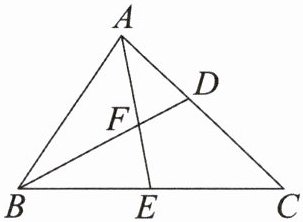
3. 如图,在$\triangle ABC$中,BC边上的中线AE与$\angle ABC$的平分线BD交于点F,$AD = AF$.
(1) 求证:$CD = 2EF$;
(2) 若$DF = 2$,$\frac { A D } { C D } = \frac { \sqrt { 2 } } { 2 }$,求BF的值.
(1) 求证:$CD = 2EF$;
(2) 若$DF = 2$,$\frac { A D } { C D } = \frac { \sqrt { 2 } } { 2 }$,求BF的值.

答案:
(1) 略
(2) $2 + 2\sqrt{2}$
(1) 略
(2) $2 + 2\sqrt{2}$
查看更多完整答案,请扫码查看


