《2025年阳光同学分层设计九年级数学全一册人教版福建专版》

某商贸公司购进某种商品,这种商品的进价为20元/kg.经过市场调研,整理出这种商品在第x$(1≤x≤48)$天的售价与日销售量的相关信息如表.设销售这种商品的日销售利润为y元.
(1)求y与x的函数解析式.
(2)第几天的日销售利润最大？最大日销售利润为多少？

答案：
(1)$y=\left\{\begin{array}{l} -2x^{2}+100x+1200,1≤x＜30,\\ -80x+4800,30≤x≤48\end{array}\right. $
![img alt=2]
(2)第 25 天的日销售利润最大,最大日销售利润为 2 450 元

(2025龙岩长汀联考)某公司投入20万元作为某种电子产品的研发费用,这种电子产品研发成功后投入生产并进行销售.已知生产这种电子产品的成本为10元/件,公司规定该种电子产品每件的销售价格不低于22元,不高于32元.在销售过程中发现：销售量y(单位：万件)与销售价格x(单位：元/件)的关系如图所示.设该公司销售这种电子产品的利润为S(单位：万元).
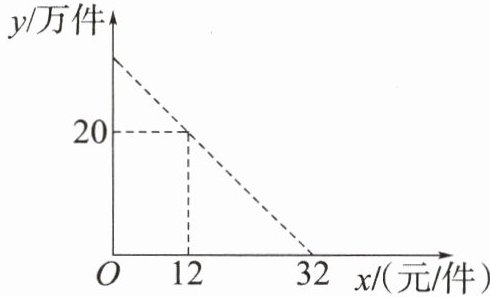
(1)求销售量y(单位：万件)与销售价格x(单位：元/件)之间的函数解析式；
(2)求销售这种电子产品的利润的最大值(利润= 总售价一总成本一研发费用)；
(3)公司决定每销售1件这种电子产品就捐赠m元$(m≥5)$给希望工程,通过销售记录发现,销售价格大于25元/件时,扣除捐赠后的利润随销售价格x(x为正整数)的增大而减小,求m的取值范围.

答案：
(1)$y=-x+32$
(2)100 万元
(3)$5≤m≤8$