《2025年阳光同学分层设计九年级数学全一册人教版福建专版》

1. 如图,抛物线$y= ax^{2}+c(a＞0)与x轴交于A$,$B$两点(点$A在点B$左侧),与$y轴负半轴交于点C$,且$OB= 2OC$,连接$AC$,$BC$,$S_{\triangle ABC}= 2$。
(1)求抛物线的函数解析式；
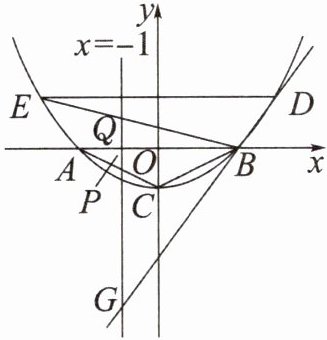
(2)$D是点B$右侧抛物线上的一动点,$D$,$E两点关于y$轴对称,直线$DB$,$EB分别交直线x= -1于G$,$Q$两点,$GQ交x轴于点P$,求$PG-PQ$的值。

答案：
(1) $ y = \frac { 1 } { 4 } x ^ { 2 } - 1 $
(2) $ P G - P Q $ 的值为 3

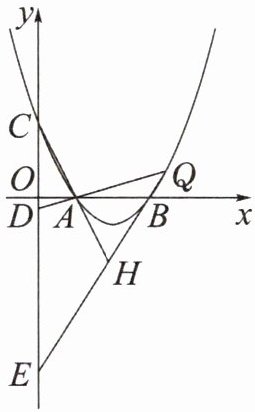
2. 如图,抛物线$y= ax^{2}-4ax+3a(a＞0)交x轴正半轴于A$,$B$两点(点$A在点B$的左侧),交$y轴于点C$。若点$Q为点B$右侧抛物线上的动点,直线$QA$,$QB分别交y轴于点D$,$E$,判断$\frac {CD}{DE}$是否为定值,并说明理由。

答案： $ \frac { C D } { D E } $ 是定值，理由略