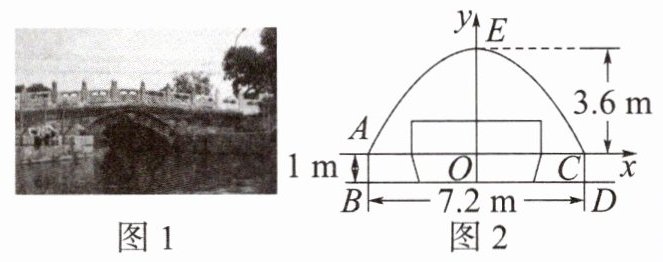
1. 万宁桥被誉为“中轴线上第一桥”,是北京中轴线15个遗产构成要素之一,是中轴线上最古老的桥梁,也是北京市目前唯一还在为社会交通服务的元代桥梁,其示意图如图1所示. 万宁桥为单孔拱券桥,桥拱截面可近似看成抛物线,建立平面坐标系,如图2所示,桥拱净跨度AC约为7.2m,拱高OE约为3.6m,桥拱底端到水面的距离AB约为1m.
(1)求该抛物线的解析式.
(2)现有一艘游船在水面上航行,其左右两边缘最宽处有一个长方体形状的遮阳棚. 水面到棚顶的高度为2.5m,遮阳棚的宽为4m,如图2所示. 此船能否从桥洞的正中央驶过?请说明理由.
(1)求该抛物线的解析式.
(2)现有一艘游船在水面上航行,其左右两边缘最宽处有一个长方体形状的遮阳棚. 水面到棚顶的高度为2.5m,遮阳棚的宽为4m,如图2所示. 此船能否从桥洞的正中央驶过?请说明理由.

答案:
(1) $ y = -\frac{5}{18}x^{2} + 3.6 $
(2) 能从桥洞的正中央驶过,理由略
(1) $ y = -\frac{5}{18}x^{2} + 3.6 $
(2) 能从桥洞的正中央驶过,理由略
2. 护林员在一个斜坡上的点A处安装自动浇灌装置(其高度忽略不计)为坡地AB进行浇灌,OA= 10m,点A处的自动浇灌装置喷出的水柱呈抛物线形. 当水柱在距出水口A的水平距离为6m时,达到距离地面OB的竖直高度的最大值为13m. 设喷出的水柱距出水口的水平距离为x m,距地面的竖直高度为y m,以坡底B所在的水平方向为x轴,A处所在的竖直方向为y轴建立平面直角坐标系,原点为O,如图所示. 经过测量,可知斜坡AB的函数解析式近似为$y= -\frac{1}{2}x+10.(1)$求图中水柱所在抛物线的函数解析式.
(2)水柱能覆盖整个坡地AB吗?若能,请说明理由;若不能,请给该浇灌装置安装一个支架,用于调节浇灌装置的高度,使得喷出的水柱恰好可以覆盖整个坡地AB,并求出安装的支架的高度.

(2)水柱能覆盖整个坡地AB吗?若能,请说明理由;若不能,请给该浇灌装置安装一个支架,用于调节浇灌装置的高度,使得喷出的水柱恰好可以覆盖整个坡地AB,并求出安装的支架的高度.

答案:
(1) $ y = -\frac{1}{12}(x - 6)^{2} + 13 $
(2) 不能,安装的支架的高度为 $\frac{10}{3}m$
(1) $ y = -\frac{1}{12}(x - 6)^{2} + 13 $
(2) 不能,安装的支架的高度为 $\frac{10}{3}m$
查看更多完整答案,请扫码查看


