1. 如图,已知$AB = AC = AD,∠CBD = 2∠BDC,∠BAC = 42^{\circ }$,则$∠CAD$的度数是____.


答案:
$ 84 ^ { \circ } $
2. 如图,在边长为 2 的菱形 ABCD 中,$∠A = 60^{\circ }$,M 是边 AD 的中点,N 是边 AB 上的一动点.若将$△AMN$沿 MN 所在直线翻折得到$△A'MN$,连接$A'C$,则$A'C$长度的最小值是____.


答案:
$ \sqrt { 7 } - 1 $
3. 如图,在$△ABC$中,$∠ABC = 90^{\circ },BC = 2AB = 4$,点 D 为平面内一动点,且$AD = 1$,E 为 CD 的中点,则 BE 的最大值为____.
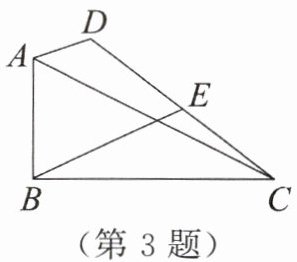

答案:
$ \sqrt { 5 } + \frac { 1 } { 2 } $
4. 如图,在$Rt△ABC$中,M 是斜边 AB 的中点,将线段 MA 绕点 M 旋转至 MD 的位置,点 D 在直线 AB 外,连接 AD,BD.
(1)如图 1 所示.
①求$∠ADB$的度数;
②若 AD 平分$∠CAB$,求证:$MD⊥BC$.
(2)如图 2,已知点 D 和边 AC 上的点 E 满足$ME⊥AD$于点 F,$DE// AB,EF = \sqrt {3}$,连接 CD,求 CD 的长.
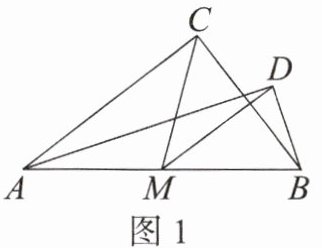

(1)如图 1 所示.
①求$∠ADB$的度数;
②若 AD 平分$∠CAB$,求证:$MD⊥BC$.
(2)如图 2,已知点 D 和边 AC 上的点 E 满足$ME⊥AD$于点 F,$DE// AB,EF = \sqrt {3}$,连接 CD,求 CD 的长.


答案:
(1) ① $ 90 ^ { \circ } $ ②略
(2) $ 2 \sqrt { 3 } $
(1) ① $ 90 ^ { \circ } $ ②略
(2) $ 2 \sqrt { 3 } $
查看更多完整答案,请扫码查看


