第88页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
1 认真想,仔细填。
(1)①一个长2毫米的精密零件,画在图纸上长3.2厘米,这幅图的比例尺是(
②南京长江大桥的铁路桥约长6800米,画在比例尺是1:200000的图上,长度约是(
(2)0.8、2、5和x能组成比例,x最大是(
(3)下面各信息中的两种量,(
①行驶5千米所用的时间和平均速度;②社团人数一定,出勤人数和缺勤人数;③分数值一定,它的分子和分母;④在一幅条形统计图中,直条的长度和直条所表示的数量;⑤圆的周长和圆周率;⑥x:5=6:y(x、y均大于0),x和y。
(1)①一个长2毫米的精密零件,画在图纸上长3.2厘米,这幅图的比例尺是(
$16:1$
)。②南京长江大桥的铁路桥约长6800米,画在比例尺是1:200000的图上,长度约是(
3.4
)厘米。(2)0.8、2、5和x能组成比例,x最大是(
12.5
),最小是(0.32
)。(3)下面各信息中的两种量,(
③④
)成正比例,(①⑥
)成反比例,(②⑤
)不成比例。(填序号)①行驶5千米所用的时间和平均速度;②社团人数一定,出勤人数和缺勤人数;③分数值一定,它的分子和分母;④在一幅条形统计图中,直条的长度和直条所表示的数量;⑤圆的周长和圆周率;⑥x:5=6:y(x、y均大于0),x和y。
答案:
1.
(1)①$16:1$ ②3.4
(2)12.5 0.32
(3)③④ ①⑥ ②⑤
(1)①$16:1$ ②3.4
(2)12.5 0.32
(3)③④ ①⑥ ②⑤
2 解比例。
25%:5=x:8
$ \frac{3.6}{x}=\frac{0.8}{1.2} $
$ \frac{4}{7}:\frac{2}{3}=\frac{3}{7}:x $
25%:5=x:8
$ \frac{3.6}{x}=\frac{0.8}{1.2} $
$ \frac{4}{7}:\frac{2}{3}=\frac{3}{7}:x $
答案:
2. $x=0.4$ $x=5.4$ $x=\frac{1}{2}$
3 一辆汽车从A城开往B城,计划每小时行驶80千米,5小时可以到达。如果这辆汽车要提早1小时到达B城,那么平均每小时要行驶多少千米?
答案:
3. 解:设平均每小时要行驶 x 千米。
$(5-1)x=5×80$
$x=100$
答:平均每小时要行驶 100 千米。
$(5-1)x=5×80$
$x=100$
答:平均每小时要行驶 100 千米。
4 一辆慢车和一辆快车沿相同路线从A地到B地,所行的路程与时间的关系如下图所示。
(1)慢车所行的路程与时间成(
(2)快车追上慢车用了(
(3)A、B两地之间的路程是(
(4)快车从A地到B地用了(
(5)点(8,400)在(
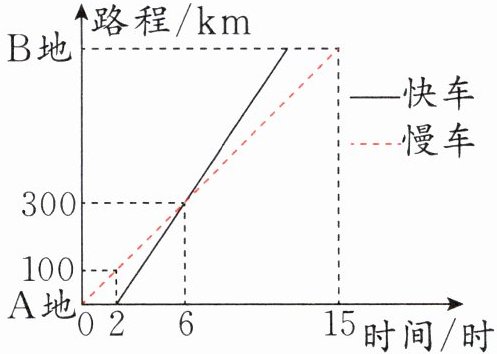
(1)慢车所行的路程与时间成(
正
)比例。(2)快车追上慢车用了(
4
)小时。(3)A、B两地之间的路程是(
750
)千米。(4)快车从A地到B地用了(
10
)小时。(5)点(8,400)在(
虚
)线上(填“实”或“虚”),它表示(慢车 8 小时行驶了 400 千米
)。
答案:
4.
(1)正
(2)4
(3)750
(4)10
(5)虚 慢车 8 小时行驶了 400 千米
(1)正
(2)4
(3)750
(4)10
(5)虚 慢车 8 小时行驶了 400 千米
5 甲、乙、丙三个村合修一条道路,三个村所修长度的比为8:7:5,且要按所修长度之比派遣劳动力。丙村由于特殊原因,没有派遣劳动力,但需付给甲、乙两村劳动报酬共1500元。最后甲村派出50人,乙村派出30人,甲、乙两村各应分得多少元?
答案:
5. $(50+30)÷(8+7+5)=4$(人)
$50-8×4=18$(人) $30-7×4=2$(人)
$18:2=9:1$
甲村应分得的钱:$1500×\frac{9}{9+1}=1350$(元)
乙村应分得的钱:$1500-1350=150$(元)
答:甲村应分得 1350 元,乙村应分得 150 元。
解析 步骤一 根据三个村所修长度的比为$8:7:5$,可把道路看成$8+7+5=20$(份)。
步骤二 甲、乙两村共派出劳动力$50+30=80$(人),每份道路需劳动力$80÷20=4$(人)。甲村应修 8 份,需劳动力$8×4=32$(人);乙村应修 7 份,需劳动力$7×4=28$(人)。
步骤三 甲村多派出$50-32=18$(人);乙村多派出$30-28=2$(人)。甲村多派的 18 人和乙村多派的 2 人帮助丙村修路,应将丙村支付的钱数按$18:2$(即$9:1$)进行分配。
$50-8×4=18$(人) $30-7×4=2$(人)
$18:2=9:1$
甲村应分得的钱:$1500×\frac{9}{9+1}=1350$(元)
乙村应分得的钱:$1500-1350=150$(元)
答:甲村应分得 1350 元,乙村应分得 150 元。
解析 步骤一 根据三个村所修长度的比为$8:7:5$,可把道路看成$8+7+5=20$(份)。
步骤二 甲、乙两村共派出劳动力$50+30=80$(人),每份道路需劳动力$80÷20=4$(人)。甲村应修 8 份,需劳动力$8×4=32$(人);乙村应修 7 份,需劳动力$7×4=28$(人)。
步骤三 甲村多派出$50-32=18$(人);乙村多派出$30-28=2$(人)。甲村多派的 18 人和乙村多派的 2 人帮助丙村修路,应将丙村支付的钱数按$18:2$(即$9:1$)进行分配。
查看更多完整答案,请扫码查看


