第50页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
五、解决问题。
1. 把一个物体分成两部分,当较长的部分与整体的长度比是 $0.618:1$ 时,给人的感觉是最美的,这个神奇的比被称为“黄金比”。
(1) 请利用“黄金比”和图 1 中正五角星的数据,写出一个比例。
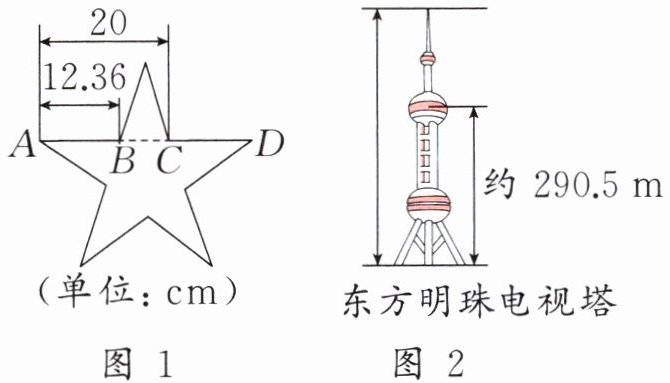
(2) 东方明珠电视塔的美就体现了“黄金比”。请你根据图 2 中的数据求出从塔尖到地面的距离约是多少米。(得数保留整米数)
(3) 把东方明珠电视塔画在比例尺为$\frac{1}{2000}$的图纸上,则塔尖到地面的距离要画多少厘米?
1. 把一个物体分成两部分,当较长的部分与整体的长度比是 $0.618:1$ 时,给人的感觉是最美的,这个神奇的比被称为“黄金比”。
(1) 请利用“黄金比”和图 1 中正五角星的数据,写出一个比例。

(2) 东方明珠电视塔的美就体现了“黄金比”。请你根据图 2 中的数据求出从塔尖到地面的距离约是多少米。(得数保留整米数)
(3) 把东方明珠电视塔画在比例尺为$\frac{1}{2000}$的图纸上,则塔尖到地面的距离要画多少厘米?
答案:
1.
(1)
由题意得比例:$12.36:20=0.618:1$。
(2)
设从塔尖到地面的距离约是$x$米,
由黄金比可得:$x:290.5 = 1:0.618$,
则$x\approx470$。
(3)
$470.24\approx470$,
$470×\frac{1}{2000}=0.235(m)$,
$0.235 m = 23.5 cm$。
综上,正确答案为:$23.5$。
(1)
由题意得比例:$12.36:20=0.618:1$。
(2)
设从塔尖到地面的距离约是$x$米,
由黄金比可得:$x:290.5 = 1:0.618$,
则$x\approx470$。
(3)
$470.24\approx470$,
$470×\frac{1}{2000}=0.235(m)$,
$0.235 m = 23.5 cm$。
综上,正确答案为:$23.5$。
2. 我国古代钱币的形制有的为外圆内方,寓意天圆地方。街口有一个按铜钱(图 1)放大的模型,图 2 为从模型上面看到的形状,要想让一个成年人轻松钻进模型中间的正方形洞,洞的边长至少是 1 米。算一算,一个成年人能轻松钻进这个洞吗?
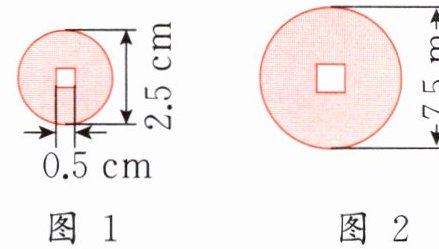
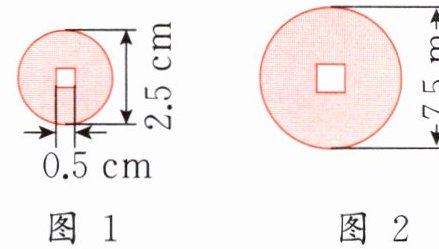
答案:
由图1可知,铜钱直径为$2.5$cm,中间正方形边长$0.5$cm,
图2中铜钱直径放大到$7.5$m,
放大比值为$\frac{7.5\mathrm{m}}{2.5\mathrm{cm}} = 300$,
所以中间正方形边长也放大$300$倍,
即$0.5\mathrm{cm} × 300 = 1.5\mathrm{m}$,
$1.5\mathrm{m} > 1\mathrm{m}$。
答:一个成年人能轻松钻进这个洞。
图2中铜钱直径放大到$7.5$m,
放大比值为$\frac{7.5\mathrm{m}}{2.5\mathrm{cm}} = 300$,
所以中间正方形边长也放大$300$倍,
即$0.5\mathrm{cm} × 300 = 1.5\mathrm{m}$,
$1.5\mathrm{m} > 1\mathrm{m}$。
答:一个成年人能轻松钻进这个洞。
3. 在比例尺为 $1:5000000$ 的地图上,量得 A、B 两地间的距离是 5 厘米。甲、乙两车分别从两地同时开出,相向而行,经过 2 小时相遇。已知甲、乙两车的速度之比是 $2:3$,则甲、乙两车每小时分别行驶多少千米?
答案:
答题卡作答:
实际距离:$5×5000000 = 25000000$(厘米),$25000000$厘米$ = 250$千米。
速度和:$250÷2 = 125$(千米/时)。
甲车速度:$125×\frac{2}{2 + 3}= 50$(千米/时)。
乙车速度:$125×\frac{3}{2 + 3}= 75$(千米/时)。
答:甲车每小时行驶50千米,乙车每小时行驶75千米。
实际距离:$5×5000000 = 25000000$(厘米),$25000000$厘米$ = 250$千米。
速度和:$250÷2 = 125$(千米/时)。
甲车速度:$125×\frac{2}{2 + 3}= 50$(千米/时)。
乙车速度:$125×\frac{3}{2 + 3}= 75$(千米/时)。
答:甲车每小时行驶50千米,乙车每小时行驶75千米。
4. 为进一步传承和弘扬中华优秀传统文化,丰富校园文化生活,提高学生的汉字书写能力和书法艺术水平,淮海小学开展“书法进校园”活动,现场为学生进行专业书法指导。该活动共有 85 名同学参加,其中女生人数的$\frac{2}{3}$与男生人数的$\frac{3}{4}$相等。活动中男生和女生各有多少人?


答案:
设女生人数为$x$,男生人数为$y$。
根据题意,总人数为85,即:
$x + y = 85$,
女生人数的$\frac{2}{3}$与男生人数的$\frac{3}{4}$相等,即:
$\frac{2}{3}x = \frac{3}{4}y$,
将方程$\frac{2}{3}x = \frac{3}{4}y$两边同时乘以12(即3和4的最小公倍数)以消去分数:
$8x = 9y$,
解这个方程,得到:
$x = \frac{9}{8}y$,
将$x = \frac{9}{8}y$代入$x + y = 85$中,得到:
$\frac{9}{8}y + y = 85$,
$\frac{17}{8}y = 85$,
$y = 40$,
将$y = 40$代入$x = \frac{9}{8}y$,得到:
$x = \frac{9}{8} × 40$,
$x = 45$,
答:女生有45人,男生有40人。
根据题意,总人数为85,即:
$x + y = 85$,
女生人数的$\frac{2}{3}$与男生人数的$\frac{3}{4}$相等,即:
$\frac{2}{3}x = \frac{3}{4}y$,
将方程$\frac{2}{3}x = \frac{3}{4}y$两边同时乘以12(即3和4的最小公倍数)以消去分数:
$8x = 9y$,
解这个方程,得到:
$x = \frac{9}{8}y$,
将$x = \frac{9}{8}y$代入$x + y = 85$中,得到:
$\frac{9}{8}y + y = 85$,
$\frac{17}{8}y = 85$,
$y = 40$,
将$y = 40$代入$x = \frac{9}{8}y$,得到:
$x = \frac{9}{8} × 40$,
$x = 45$,
答:女生有45人,男生有40人。
查看更多完整答案,请扫码查看


