《2026年53天天练六年级数学下册苏教版》

3 任务三：这样的规律是否适用于其他形状的多边形？
提出猜想
通过前面的探究，我猜想其他形状的多边形也有这样的规律：将其他形状的多边形按一定的比放大或缩小后，对应角的度数(相等)(填“相等”或“不相等”)，对应边的长度比(能)组成比例(填“能”或“不能”)。
举例论证
操作步骤：
① 画一画：任意画一个六边形，再画出这个六边形按比放大和按比缩小后的图形。
② 量一量：分别量出三个六边形中各角的度数和各边的长度，并在图上标一标。
③ 算一算：对应边的长度比能组成比例吗？
规律总结
通过测量、计算，我发现：
将多边形按一定的比放大或缩小后，对应角的度数(相等)(填“相等”或“不相等”)，对应边的长度比(能)组成比例(填“能”或“不能”)。

答案： 3. 相等 能 举例论证略。 相等 能

我的结论
将图形按一定的比放大或缩小后，图形的大小改变，形状不变，对应角的度数(相等)(填“相等”或“不相等”)，对应边的长度比(能)组成比例(填“能”或“不能”)，我们把这两个图形叫作相似图形。

答案： 我的结论
相等 能

1 如下图，在长方形 $ABCD$ 中，点 $E$、$F$ 分别在边 $AB$、$BC$ 上，三角形 $ADE$ 和三角形 $BEF$ 是相似图形。已知 $AB = 20$ 厘米，$AD = 12$ 厘米，$AE = 15$ 厘米，求 $FC$ 的长度。

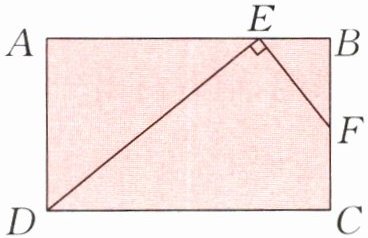
答案： 1. EB 的长度：20−15=5（厘米）
解：设 BF 的长度是 x 厘米。
15∶x=12∶5
x=6.25
FC 的长度：12−6.25=5.75（厘米）
答：FC 的长度是 5.75 厘米。

2 如下图，三角形 $ACD$ 是等腰三角形，三角形 $CBD$ 和三角形 $ABC$ 是相似图形。与 $∠ A$ 度数相等的角是哪个角？$∠ ACB$ 的度数是多少？

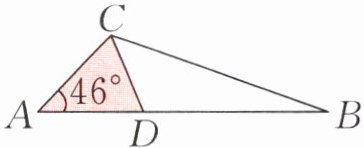
答案： 2. ∠BCD=∠A=46°
∠ACD：(180°−46°)÷2=67°
∠ACB：46°+67°=113°
答：与∠A 度数相等的角是∠BCD。
∠ACB 的度数是 113°。