第15页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
1 如图,将一个高为h、底面半径为r的圆柱平均分成若干份,然后拼成一个近似的长方体。
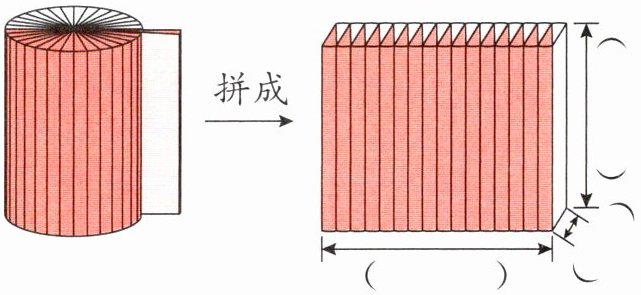
(1)用含r、h的式子在长方体上标注尺寸。
(2)长方体与圆柱相比,底面积(
(3)长方体的体积=底面积×高,所以圆柱的体积用含r、h的式子表示为V=(

(1)用含r、h的式子在长方体上标注尺寸。
(2)长方体与圆柱相比,底面积(
不变
),高(不变
),体积(不变
)。(填“不变”“变大”或“变小”)(3)长方体的体积=底面积×高,所以圆柱的体积用含r、h的式子表示为V=(
πr²h
)。
答案:
1.
(1)(从左到右)πr r h
(2)不变 不变 不变
(3)πr²h
(1)(从左到右)πr r h
(2)不变 不变 不变
(3)πr²h
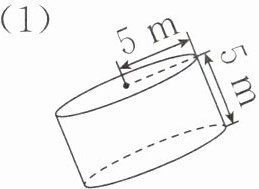
2 计算下面圆柱的体积。
(1)
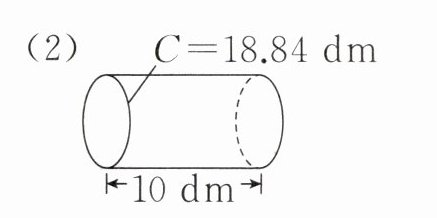
(2)
(1)

(2)

答案:
2.
(1)3.14×5²×5=392.5(m³)
(2)18.84÷3.14÷2=3(dm)
3.14×3²×10=282.6(dm³)
(1)3.14×5²×5=392.5(m³)
(2)18.84÷3.14÷2=3(dm)
3.14×3²×10=282.6(dm³)
3 一个圆柱形桥墩是由混凝土浇筑而成的,它的底面积是1.57平方米,水上部分高4米,水下部分高6米。请你算一算,浇筑这个桥墩,需要混凝土多少立方米?


答案:
3. 1.57×(4+6)=15.7(立方米)
答:需要混凝土15.7立方米。
答:需要混凝土15.7立方米。
4 一个竖直放置的圆柱形木桶的相关数据如下,这个木桶最多能盛多少升水? (得数保留整数)
①占地面积是254.34平方厘米。 ②从里面量,底面直径是16厘米。
③从里面量,最矮木板高20厘米。 ④从里面量,最高木板高25厘米。

我需要的数据有(

若该木桶桶壁的木板长短不一,则该木桶的盛水量取决于桶壁上最矮的木板,这就是“木桶效应”。
①占地面积是254.34平方厘米。 ②从里面量,底面直径是16厘米。
③从里面量,最矮木板高20厘米。 ④从里面量,最高木板高25厘米。

我需要的数据有(
②③
)(填序号),我的解答如下:
若该木桶桶壁的木板长短不一,则该木桶的盛水量取决于桶壁上最矮的木板,这就是“木桶效应”。
答案:
4. ②③
3.14×(16÷2)²×20=4019.2(立方厘米)
4019.2立方厘米=4.0192升 4.0192≈4
答:这个木桶最多能盛4升水。
3.14×(16÷2)²×20=4019.2(立方厘米)
4019.2立方厘米=4.0192升 4.0192≈4
答:这个木桶最多能盛4升水。
5 在一节数学课上,老师带来了一个圆柱形空心钢管教具,让同学们计算体积。下面是两位同学的想法,请你根据他们的想法将计算过程补充完整并观察结果。
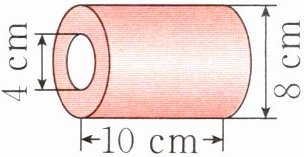
小明:用V=V大圆柱 - V小圆柱计算。
妙妙:用V=Sh计算。
我发现:

小明:用V=V大圆柱 - V小圆柱计算。
妙妙:用V=Sh计算。
我发现:
空心圆柱的体积可以用底面积乘高计算(发现合理即可)
。
答案:
5. 小明$:V=V_{大圆柱}-V_{小圆柱}=3.14×(8÷2)²×10-3.14×(4÷2)²×10=376.8(cm³)$
妙妙:S=3.14×(8÷2)²-3.14×(4÷2)²=37.68(cm²)
V=Sh=37.68×10=376.8(cm³)
空心圆柱的体积可以用底面积乘高计算(发现合理即可)
解析 根据公式代入计算即可。可以发现两种方式的计算结果相同,发现合理即可。
妙妙:S=3.14×(8÷2)²-3.14×(4÷2)²=37.68(cm²)
V=Sh=37.68×10=376.8(cm³)
空心圆柱的体积可以用底面积乘高计算(发现合理即可)
解析 根据公式代入计算即可。可以发现两种方式的计算结果相同,发现合理即可。
查看更多完整答案,请扫码查看


