第22页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
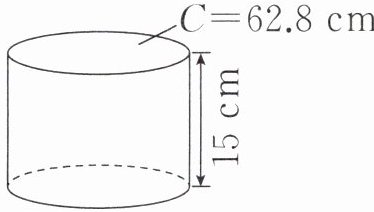
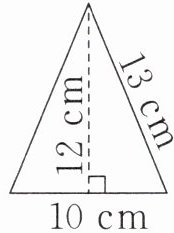
1. (1)求下面圆柱的表面积。 (2)从前面看一个圆锥,如图,求它的体积。


答案:
1.
(1)$62.8÷3.14÷2=10(cm)$
$3.14×10^{2}×2+62.8×15=1570(cm^{2})$
(2)$3.14×(10÷2)^{2}×12÷3=314(cm^{3})$
(1)$62.8÷3.14÷2=10(cm)$
$3.14×10^{2}×2+62.8×15=1570(cm^{2})$
(2)$3.14×(10÷2)^{2}×12÷3=314(cm^{3})$
2. 认真想,仔细填。
(1)如右图,一个圆柱形玻璃瓶的瓶口面积和一种圆锥形高脚杯的杯口面积相等,瓶中的饮料最多可以倒满(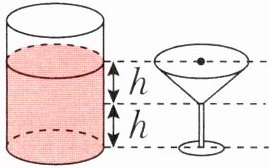
(2)李师傅做了一个圆柱形灯笼,底面直径是 10 厘米,高是 20 厘米。要给灯笼的侧面和下底面都贴上彩纸,至少需要(
(3)一个圆柱和一个圆锥的底面积相等,圆锥的高是 25 厘米,体积是 100 立方厘米;圆柱的体积是 300 立方厘米,高是(
(1)如右图,一个圆柱形玻璃瓶的瓶口面积和一种圆锥形高脚杯的杯口面积相等,瓶中的饮料最多可以倒满(
6
)个这种高脚杯。
(2)李师傅做了一个圆柱形灯笼,底面直径是 10 厘米,高是 20 厘米。要给灯笼的侧面和下底面都贴上彩纸,至少需要(
7.065
)平方分米的彩纸。(3)一个圆柱和一个圆锥的底面积相等,圆锥的高是 25 厘米,体积是 100 立方厘米;圆柱的体积是 300 立方厘米,高是(
25
)厘米。
答案:
2.
(1)6
(2)7.065
(3)25
(1)6
(2)7.065
(3)25
3. 一根长 2 米、底面直径是 20 厘米的圆柱形木头浮在水上,正好有一半露出水面(如右图)。
(1)这根木头的体积是多少立方分米? (2)木头与水接触的面积是多少平方分米?

(1)这根木头的体积是多少立方分米? (2)木头与水接触的面积是多少平方分米?

答案:
3.
(1)2米=20分米 20厘米=2分米
$3.14×(2÷2)^{2}×20=62.8$(立方分米)
答:这根木头的体积是62.8立方分米。
(2)$3.14×(2÷2)^{2}÷2×2+3.14×2×20÷2=65.94$(平方分米)
答:木头与水接触的面积是65.94平方分米。
(1)2米=20分米 20厘米=2分米
$3.14×(2÷2)^{2}×20=62.8$(立方分米)
答:这根木头的体积是62.8立方分米。
(2)$3.14×(2÷2)^{2}÷2×2+3.14×2×20÷2=65.94$(平方分米)
答:木头与水接触的面积是65.94平方分米。
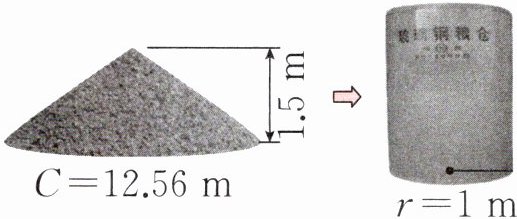
4. 粮仓是用于储存粮食的专用建筑,具备防潮、隔热、通风等性能。王叔叔要将下面这个圆锥形小麦堆全部平铺装入圆柱形粮仓中,结果最上面的小麦离仓口还有 0.5 米。这个粮仓的高是多少米?

答案:
4. $12.56÷3.14÷2=2$(米)
$\frac {1}{3}×3.14×2^{2}×1.5=6.28$(立方米)
$6.28÷(3.14×1^{2})+0.5=2.5$(米)
答:这个粮仓的高是2.5米。
$\frac {1}{3}×3.14×2^{2}×1.5=6.28$(立方米)
$6.28÷(3.14×1^{2})+0.5=2.5$(米)
答:这个粮仓的高是2.5米。
5. 在计算一个圆柱的体积时,妙妙错将底面直径当成底面半径计算,所得结果是 25.12 立方厘米。


答案:
5. 答:正确的结果是6.28立方厘米。假设圆柱的底面半径为r,高为h,则底面直径为2r。圆柱的体积应为$πr^{2}h$,妙妙错误地计算为$4πr^{2}h$,所以错误结果是正确结果的4倍,正确的结果是$25.12÷4=6.28$(立方厘米)。
6. 如图,分别以直角梯形 $ABCD$ 中 $AB$ 边和 $CD$ 边所在直线为轴旋转一周,得到立体图形①和立体图形②。
(1)以 $AB$ 边所在直线为轴进行旋转会形成立体图形(
(2)立体图形①的体积是立体图形②的 $\frac{(\ )}{(\ )}$。
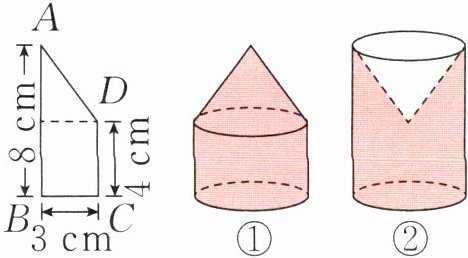
(1)以 $AB$ 边所在直线为轴进行旋转会形成立体图形(
①
)。(2)立体图形①的体积是立体图形②的 $\frac{(\ )}{(\ )}$。

答案:
6.
(1)①
(2)$\frac {4}{5}$
解析 第
(1)题,以AB边所在直线为轴旋转时,上面三角形会形成一个圆锥,下面长方形会形成一个圆柱,所以是立体图形①。
第
(2)题,本题可利用推导法解题。
步骤一 形成的立体图形中,上面的圆锥和下面的圆柱等底等高,所以圆锥体积是圆柱体积的$\frac {1}{3}$。
步骤二 若把圆柱的体积看作3,则圆锥的体积就是1,立体图形①的体积为$3+1=4$,立体图形②的体积为2倍的圆柱体积减去圆锥的体积,即$6-1=5$。
步骤三 计算结果。$4:5=\frac {4}{5}$。
![img alt=图片编号或题号(图片的具体编号或者所属题目的题号)]
(1)①
(2)$\frac {4}{5}$
解析 第
(1)题,以AB边所在直线为轴旋转时,上面三角形会形成一个圆锥,下面长方形会形成一个圆柱,所以是立体图形①。
第
(2)题,本题可利用推导法解题。
步骤一 形成的立体图形中,上面的圆锥和下面的圆柱等底等高,所以圆锥体积是圆柱体积的$\frac {1}{3}$。
步骤二 若把圆柱的体积看作3,则圆锥的体积就是1,立体图形①的体积为$3+1=4$,立体图形②的体积为2倍的圆柱体积减去圆锥的体积,即$6-1=5$。
步骤三 计算结果。$4:5=\frac {4}{5}$。
![img alt=图片编号或题号(图片的具体编号或者所属题目的题号)]
查看更多完整答案,请扫码查看


