第19页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
1 一个圆柱,底面直径是2分米,高是6分米,它的体积是(
18.84
)立方分米;一个圆锥,底面直径是2分米,高是6分米,它的体积是(6.28
)立方分米。
答案:
1. 18.84 6.28
2 计算下面圆锥的体积。
(1)
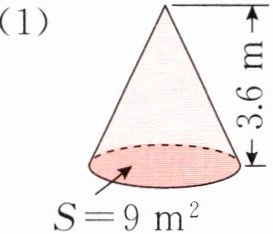
(2)
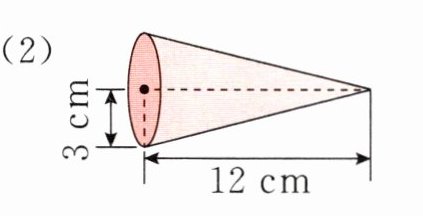
(1)

(2)

答案:
2.
(1) $ 9 × 3.6 × \frac{1}{3} = 10.8 (m^{3}) $
(2) $ 3.14 × 3^{2} × 12 × \frac{1}{3} = 113.04 (cm^{3}) $
(1) $ 9 × 3.6 × \frac{1}{3} = 10.8 (m^{3}) $
(2) $ 3.14 × 3^{2} × 12 × \frac{1}{3} = 113.04 (cm^{3}) $
3 “斜仁柱”又称“撮罗子”或“撮罗昂库”,是鄂伦春族、鄂温克族、赫哲族等民族游猎时期居住的一种圆锥形的临时“房子”。下图中这个“斜仁柱”的底面直径是4米,高是3米。
(1)这个“斜仁柱”的占地面积是(
(2)这个“斜仁柱”内的空间有多大?(厚度忽略不计)

(1)这个“斜仁柱”的占地面积是(
12.56
)平方米。(2)这个“斜仁柱”内的空间有多大?(厚度忽略不计)

答案:
3.
(1) 12.56
(2) $ 12.56 × 3 × \frac{1}{3} = 12.56 $ (立方米)
答:这个“斜仁柱”内的空间有 12.56 立方米。
(1) 12.56
(2) $ 12.56 × 3 × \frac{1}{3} = 12.56 $ (立方米)
答:这个“斜仁柱”内的空间有 12.56 立方米。
4 “甜甜向上”甜品店推出一款新口味的冰沙,为满足不同客户群体的需求,商家为这款冰沙设计了两种包装,两种包装及定价如下图所示。(每种包装中的冰沙都刚好装满)
(1)你认为这样的定价合理吗?若不合理,则请你结合数据给出定价建议。
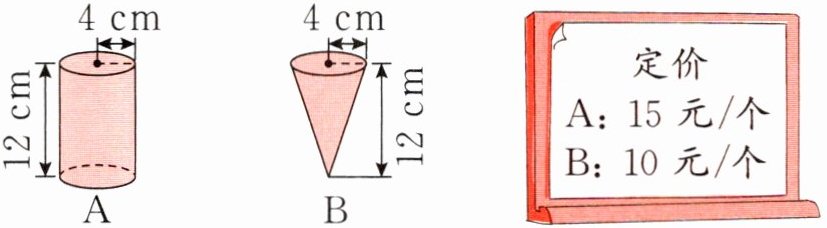
(2)一位顾客下单了3个B款冰沙,店员大约要用多少立方厘米的冰沙?

(1)你认为这样的定价合理吗?若不合理,则请你结合数据给出定价建议。

(2)一位顾客下单了3个B款冰沙,店员大约要用多少立方厘米的冰沙?

答案:
4.
(1) $ 15 × \frac{1}{3} = 5 $ (元/个)
答:我认为这样的定价不合理。圆锥的体积是与它等底等高的圆柱体积的 $ \frac{1}{3} $,所以 B 款的定价也应该是 A 款的 $ \frac{1}{3} $。可以把 B 款定价改为 5 元/个。(建议合理即可)
(2) $ 3.14 × 4^{2} × 12 × \frac{1}{3} × 3 \approx 603 $ (立方厘米)
答:店员大约要用 603 立方厘米的冰沙。
(1) $ 15 × \frac{1}{3} = 5 $ (元/个)
答:我认为这样的定价不合理。圆锥的体积是与它等底等高的圆柱体积的 $ \frac{1}{3} $,所以 B 款的定价也应该是 A 款的 $ \frac{1}{3} $。可以把 B 款定价改为 5 元/个。(建议合理即可)
(2) $ 3.14 × 4^{2} × 12 × \frac{1}{3} × 3 \approx 603 $ (立方厘米)
答:店员大约要用 603 立方厘米的冰沙。
5 若将一个圆锥沿高切分成完全相同的两部分(如下图所示),则表面积比原来大60平方分米。已知圆锥的高是5分米,那么圆锥的体积是多少立方分米?
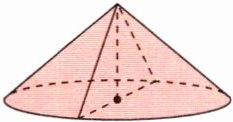

答案:
5. $ 60 ÷ 2 × 2 ÷ 5 = 12 $ (分米)
$ 3.14 × (12 ÷ 2)^{2} × 5 × \frac{1}{3} = 188.4 $ (立方分米)
答:圆锥的体积是 188.4 立方分米。
![img alt=解析]
解析 将圆锥切开后,增加的表面积是两个相同三角形(底边长 = 圆锥的底面直径,高 = 圆锥的高)的面积之和。先结合圆锥的高求出三角形的底边长,即圆锥的底面直径,再代入公式求出圆锥的体积。
$ 3.14 × (12 ÷ 2)^{2} × 5 × \frac{1}{3} = 188.4 $ (立方分米)
答:圆锥的体积是 188.4 立方分米。
![img alt=解析]
解析 将圆锥切开后,增加的表面积是两个相同三角形(底边长 = 圆锥的底面直径,高 = 圆锥的高)的面积之和。先结合圆锥的高求出三角形的底边长,即圆锥的底面直径,再代入公式求出圆锥的体积。
查看更多完整答案,请扫码查看


