《2026年53天天练六年级数学下册苏教版》

1 认真想，仔细填。
(1) (8) : 20 = 4 ÷ (10) = 0.4 = $\frac{(\ )}{5}$ = (40)%
(2) 将 5 吨 : 25 千克化成最简整数比是(200:1)，这个比的比值是(200)。
(3) 给 4 : 11 的前项加上 12，要使比值不变，应给比的后项加上(33)。
(4) 第五代移动通信技术(5G)具有高速率、低时延等特点。同一份文件，用 5G 网络下载所需时间与用 4G 网络下载所需时间的比是 1 : 20，一部影片用 4G 网络下载需要 5 分钟，那么用 5G 网络下载只需要(15)秒，所用时间缩短了(95)%。

答案： 1.
(1)8 10 2 40
(2)200:1 200
(3)33
(4)15 95

2 精挑细选。
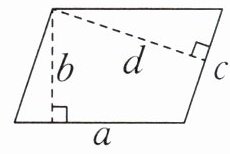
(1) 根据图中信息判断，下面选项中不成立的是(A)。
A. $a : c = b : d$
B. $a : c = d : b$
C. $\frac{b}{d} = \frac{c}{a}$
D. $\frac{a}{d} = \frac{c}{b}$

(2) “宫、商、角、徵、羽”是我国古代音乐的基本音阶。其中“徵”和“宫”的发音管长度的比是 2 : 3，“商”和“徵”的发音管长度的比是 4 : 3，则“商”“宫”和“徵”的发音管长度的比是(C)。
A. 4 : 3 : 2
B. 2 : 3 : 4
C. 8 : 9 : 6
D. 6 : 9 : 8
(3) 如图，正方形内部是太极图，它是数形结合的典范。正方形与黑色部分的面积比是(D)。
A. $π : 2$
B. $2 : π$
C. $4 : π$
D. $8 : π$

答案： 2.
(1)A
(2)C
(3)D

3 一个长方体的棱长总和是 192 厘米，长、宽、高的比是 5 : 4 : 3。求这个长方体的体积。

答案： 3. 192÷4=48(厘米)
48×$\frac{5}{5+4+3}$=20(厘米)
48×$\frac{4}{5+4+3}$=16(厘米)
48×$\frac{3}{5+4+3}$=12(厘米)
20×16×12=3840(立方厘米)
答:这个长方体的体积是3840立方厘米。

4 赵磊看一本书，已看的页数与剩下的页数的比是 3 : 4。如果再看 72 页，那么正好看完全书的$\frac{6}{7}$。这本书一共有多少页？

答案： 4. 3+4=7 72÷($\frac{6}{7}$-$\frac{3}{7}$)=168(页)
答:这本书一共有168页。

5 沙漏是古时候常用的一种计量时间的装置，不同的计时沙漏对应不同的时间。现将一个沙漏倒置，过了几分钟，发现漏下的和未漏下的沙子的体积比是 1 : 5，又过了 10 分钟，漏下的和未漏下的沙子的体积比是 1 : 2。这是一个(60)分钟沙漏。

“20 分钟沙漏”是将沙漏倒置后，经过 20 分钟，所有的沙子能从上部漏到下部。

答案： 5. 60
解析 步骤一 过了几分钟,发现漏下的和未漏下的沙子的体积比是1:5,即漏下的沙子是沙子总量的$\frac{1}{1+5}$。
步骤二 又过了10分钟,漏下的和未漏下的沙子的体积比是1:2,即漏下的沙子是沙子总量的$\frac{1}{1+2}$。
步骤三 漏下的沙子由沙子总量的$\frac{1}{1+5}$到$\frac{1}{1+2}$,经过时间为10分钟。那么漏下全部沙子需要10÷($\frac{1}{1+2}$-$\frac{1}{1+5}$)=60(分),即这是一个60分钟沙漏。