《2026年53天天练六年级数学下册苏教版》

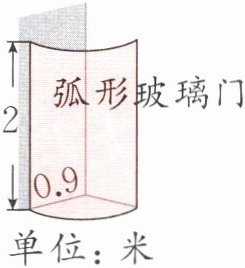
5 卫生间做到“干湿分离”可保持沐浴之外的场地干燥、卫生。奇奇家要在卫生间墙角的淋浴处靠墙做一扇弧形玻璃门(两墙夹角$90^{\circ}$，如图)，玻璃门与天花板留有一定的距离，便于淋浴时水蒸气的排出。奇奇爸爸计划自己购买材料，至少需要玻璃多少平方米？

答案： 5. $2×3.14×0.9×2÷4=2.826$(平方米)
答:至少需要玻璃 2.826 平方米。

6 涵涵用不同方法测量一个不规则小石块的体积，如下图。

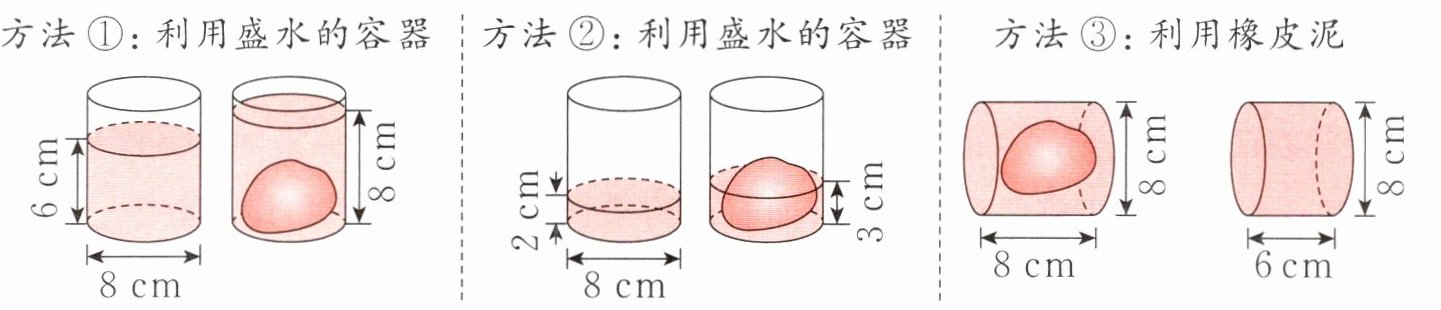
方法①：利用盛水的容器 方法②：利用盛水的容器 方法③：利用橡皮泥
(1)不能测量出这个不规则小石块的体积的是方法(②)。(填序号)
(2)请你选择一种合理且自己喜欢的方法，计算小石块的体积。

答案： 6.
(1)②
(2)示例:我选择方法①。
$3.14×(8÷2)^{2}×(8 - 6)=100.48$(立方厘米)
答:小石块的体积是 100.48 立方厘米。

7 竹筒饭是以香米和肉类为原料，将其放进新鲜的粉竹或山竹锯成的竹筒中而制成的一种美味食品。妈妈做竹筒饭的信息如下表。(竹筒的厚度忽略不计)


算一算，每根竹筒的长是多少厘米？

答案： 7. $288÷3÷\frac{4}{5}÷12=10$(厘米)
答:每根竹筒的长是 10 厘米。

8 在五年级时，我们用两个完全相同的梯形拼成平行四边形，推导出了梯形的面积公式(如下面左图)。照这样的思路，你能求出下面右图中这个几何体的体积吗？

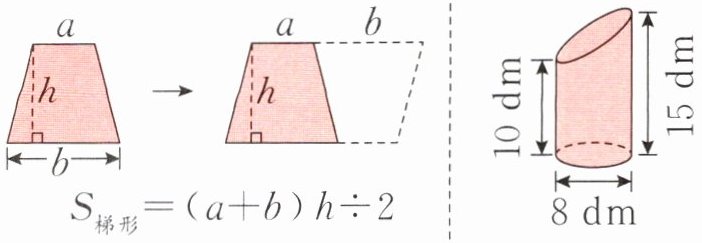
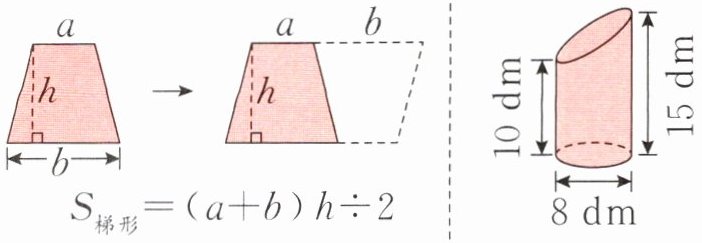
$S_{梯形} = (a + b) h ÷ 2$

答案： 8. $3.14×(8÷2)^{2}×(15 + 10)÷2=628$(立方分米)
答:这个几何体的体积是 628 立方分米。
解析 题图中的几何体相当于一个圆柱的一半,这个圆柱的底面直径是 8 分米,高是$(15 + 10)$分米。该几何体的体积是这个圆柱的一半,列式并计算即可。