《2026年53天天练六年级数学下册苏教版》

5. 关于“比例”，下面四种说法中正确的()。
①如果 $mn$ 的积是 3.2，那么 $2:m$ 和 $n:1.6$ 一定能组成比例。($m$、$n$ 均大于 0)
②一个比的前项和后项都扩大到原来的 5 倍后，得到一个新的比，这两个比能组成比例。
③在 $a:7=c:2$ 中($a$、$c$ 均大于 0)，交换两个内项的位置后，比例仍然成立。
④任意两个大小不相同的圆的周长和半径的比都可以组成比例。

A.只有①④
B.只有①②④
C.只有②③
D.有①②③④

答案： D

6. 如图，一个三角形的$\frac{1}{3}$和一个圆的$\frac{1}{5}$重叠。已知这个三角形空白部分的面积是 15 平方厘米，那么这个圆的面积是()平方厘米。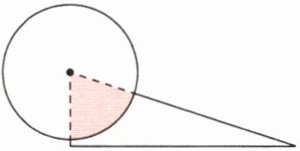

答案： 37.5

三、解比例。
$\frac{3}{4}:x=4:5$
$\frac{3}{8}x:\frac{3}{5}=1:\frac{1}{10}$
$\frac{1.6}{0.2}=\frac{1.2}{x}$
$(x+5):1.8=\frac{3}{2}:\frac{3}{10}$

答案： 一、解：
根据比例内项之积等于外项之积，由$\frac{3}{4}:x = 4:5$可得：
$4x=\frac{3}{4}×5$
$4x=\frac{15}{4}$
$x=\frac{15}{4}÷4$
$x=\frac{15}{16}$
二、解：
由$\frac{3}{8}x:\frac{3}{5}=1:\frac{1}{10}$，根据比例性质可得：
$\frac{1}{10}×\frac{3}{8}x=\frac{3}{5}×1$
$\frac{3}{80}x=\frac{3}{5}$
$x=\frac{3}{5}÷\frac{3}{80}$
$x = 16$
三、解：
由$\frac{1.6}{0.2}=\frac{1.2}{x}$，根据比例性质可得：
$1.6x = 0.2×1.2$
$1.6x = 0.24$
$x = 0.24÷1.6$
$x = 0.15$
四、解：
由$(x + 5):1.8=\frac{3}{2}:\frac{3}{10}$，根据比例性质可得：
$\frac{3}{10}(x + 5)=1.8×\frac{3}{2}$
$\frac{3}{10}(x + 5)=2.7$
$x + 5=2.7÷\frac{3}{10}$
$x + 5 = 9$
$x = 9 - 5$
$x = 4$
答案依次为$x=\frac{15}{16}$；$x = 16$；$x = 0.15$；$x = 4$。

四、操作。

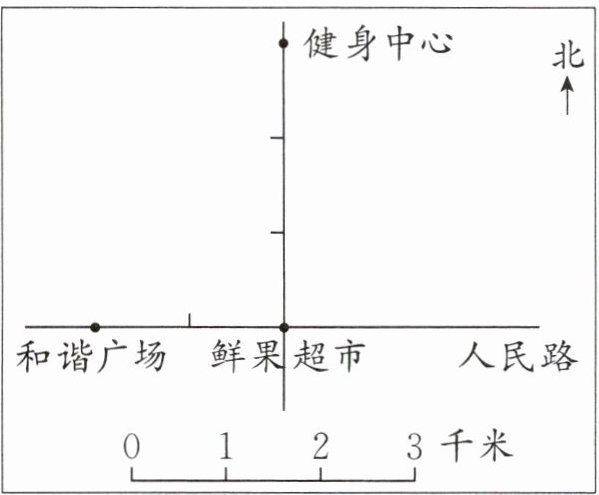
1. 右面是幸福街区的平面示意图。
(1) 和谐广场在鲜果超市的()方向()米处。
(2) 少年宫在鲜果超市的正东方向 2 千米处，请用“·”在图中标出少年宫的位置。
(3) 和平路在人民路北面，与人民路相距 2.5 千米，且与人民路平行，请在图上画出和平路。

答案：
(1) 正西 2000
(2) （在鲜果超市正东方向图上2个单位长度处标“·”）
(3) （在人民路北面图上2.5个单位长度处画一条与人民路平行的直线）

2. 下面方格图中每个小方格的边长表示 1 厘米，请根据要求作图。

(1) 画一个周长是 32 厘米的长方形，长和宽的比是 $5:3$。
(2) 画一个面积是 48 平方厘米的直角三角形，两条直角边的长度之比是 $2:3$。
(3) 将所画的直角三角形按 $1:4$ 的比缩小，画出缩小后的图形。
(4) 大直角三角形和小直角三角形的周长之比是()：()。

答案：
(1)
长方形周长 = 2×(长 + 宽)=32（厘米），所以长 + 宽 = 16厘米，因为长和宽的比是$5:3$，
总份数为$5 + 3=8$（份），
则一份是$16÷8 = 2$（厘米），
长为$2×5 = 10$（厘米），
宽为$2×3 = 6$（厘米），
在方格图中画长10格，宽6格的长方形。
(2)
设两条直角边分别为$2x$厘米和$3x$厘米，
根据三角形面积公式可得$\frac{1}{2}×2x×3x = 48$，
即$3x^{2}=48$，
$x^{2}=16$，
解得$x = 4$，
两条直角边分别为$2×4 = 8$（厘米）和$3×4 = 12$（厘米），
在方格图中画两条直角边分别为8格和12格的直角三角形。
(3)
原直角三角形两条直角边分别为8厘米和12厘米，按$1:4$缩小后，
两条直角边分别为$8÷4 = 2$（厘米）和$12÷4 = 3$（厘米），
画两条直角边分别为2格和3格的直角三角形。
(4)
$4:1$