《2026年53天天练六年级数学下册苏教版》

4. 蜂窝煤是用无烟煤制成的。每个蜂窝煤有12个相同的空心小圆柱，如下左图。

(1) 制作一个蜂窝煤需要用煤多少立方厘米？下面计算方法错误的是(③) )。(填序号)
①大圆柱的体积—12个小圆柱的体积
②蜂窝煤的底面积×高
③(大圆柱的底面周长—12个小圆柱的底面周长之和)×高
(2) 如上右图，现有一个圆锥形煤堆，用这堆煤可以制作多少个蜂窝煤？

答案： 4.
(1)③
(2)$ 3.14×(12÷2)^2×10 - 3.14×(2÷2)^2×10×12 = 753.6 $（立方厘米）
$ 3.14×(4÷2)^2×0.9×\frac{1}{3}=3.768 $（立方米）
3.768 立方米 = 3768000 立方厘米
$ 3768000÷753.6 = 5000 $（个）
答：用这堆煤可以制作 5000 个蜂窝煤。

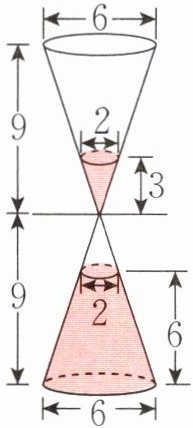
5. 沙漏是我国古代一种计量时间的仪器，根据流沙从上面漏到下面的体积来计量时间。右图是一个沙漏计量时间的情况，再过0.5分钟，沙子就全部漏下，现在沙漏已经计量了多少分钟？（单位：cm）

答案： 5. $ 3.14×(6÷2)^2×9×\frac{1}{3}=84.78 $（立方厘米）
$ 3.14×(2÷2)^2×3×\frac{1}{3}=3.14 $（立方厘米）
$ 84.78 - 3.14 = 81.64 $（立方厘米）
$ 81.64÷3.14×0.5 = 13 $（分）
答：现在沙漏已经计量了 13 分钟。

五、探究说理。
1. 为了算出一个空瓶子的容积，一个学习小组进行了实验，操作记录如下：

这个瓶子的容积约是多少立方厘米？下面是该学习小组的思路，请你列式解答。

答案： 1. $ 18.84÷3.14÷2 = 3 $（厘米）
$ 3.14×3^2×(15 + 5)=565.2 $（立方厘米）
答：这个瓶子的容积约是 565.2 立方厘米。

2. 下面是常歌收集在错题本上的一道题，请你分析一下她的错误原因，并给出正确解答。
一个装满水的圆柱形容器，底面积是80平方厘米，高是2厘米。把两根底面直径是2厘米、高是4厘米的圆柱形小棒竖直放入容器中，求从容器中溢出的水的体积。
$3.14×2^{2}×4×2 = 100.48$（立方厘米）
答：从容器中溢出的水的体积是100.48立方厘米。
★错误原因：
★正确解答：

答案： 2. 将底面直径当作底面半径计算，未考虑到小棒的高大于容器的高。
$ 3.14×(2÷2)^2×2×2 = 12.56 $（立方厘米）
答：从容器中溢出的水的体积是 12.56 立方厘米。