第41页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
1 认真想,仔细填。
(1)在比例 5:6=1.5:1.8 中,外项是(
(2)补全比例:4:10=28:(
(3)若 $a:b=12:17$,则 $a×$(
(4)右图中,平行四边形的面积可以用两种方法计算:
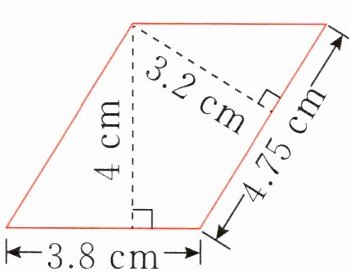
(
(
利用图中 4 个数,组成一个比例:(
(1)在比例 5:6=1.5:1.8 中,外项是(
5
)和(1.8
),内项的积是(9
)。(2)补全比例:4:10=28:(
70
) (0.03
):0.9=1.2:36 $\frac{8}{21}$:(4
)=($\frac{1}{3}$
):$\frac{7}{2}$(3)若 $a:b=12:17$,则 $a×$(
17
)$=b×$(12
);若 $4a=9b$,则 $a:b=$(9
):(4
),4:b=(9
):($a$
)。(a、b 均不为 0)(4)右图中,平行四边形的面积可以用两种方法计算:

(
3.8
)×(4
)=(15.2
)(平方厘米)(
4.75
)×(3.2
)=(15.2
)(平方厘米)利用图中 4 个数,组成一个比例:(
$\frac{3.8:3.2 = 4.75:4}$
)。
答案:
1.
(1)5 1.8 9
(2)70 0.03 4 $\frac{1}{3}$
(3)17 12 9 4 9 $a$
(4)3.8 4 15.2 4.75 3.2 15.2
$\frac{3.8:3.2 = 4.75:4}$
(本题画线部分答案不唯一)
(1)5 1.8 9
(2)70 0.03 4 $\frac{1}{3}$
(3)17 12 9 4 9 $a$
(4)3.8 4 15.2 4.75 3.2 15.2
$\frac{3.8:3.2 = 4.75:4}$
(本题画线部分答案不唯一)
2 精挑细选。
(1)在 4:6=12:18 中,如果第一个比的前项增加 12,那么第二个比的后项应该(
A. 除以 3
B. 乘 3
C. 除以 4
D. 乘 4
(2)下面说法不正确的是(
A. 交换比例的两个外项或内项,比例仍然成立
B. 能与 $\frac{7}{4}:0.7$ 组成比例的比有无数个
C. 一个比例的两个外项之积减去两个内项之积,差为 0
D. 因为 $4×9=12×3$,所以 9:12=4:3
(1)在 4:6=12:18 中,如果第一个比的前项增加 12,那么第二个比的后项应该(
C
),才能使比例仍然成立。A. 除以 3
B. 乘 3
C. 除以 4
D. 乘 4
(2)下面说法不正确的是(
D
)。A. 交换比例的两个外项或内项,比例仍然成立
B. 能与 $\frac{7}{4}:0.7$ 组成比例的比有无数个
C. 一个比例的两个外项之积减去两个内项之积,差为 0
D. 因为 $4×9=12×3$,所以 9:12=4:3
答案:
2.
(1)C
(2)D
(1)C
(2)D
3 下面哪组中的四个数可以组成比例?把组成的比例写出来(每组写一个即可)。
4,15,12 和 5
1.6,6,4.2 和 5
$\frac{1}{2}$,$\frac{1}{3}$,$\frac{1}{6}$ 和 $\frac{1}{4}$
4,15,12 和 5
1.6,6,4.2 和 5
$\frac{1}{2}$,$\frac{1}{3}$,$\frac{1}{6}$ 和 $\frac{1}{4}$
答案:
3. 答:第1、3组可以组成比例,组成的比例分别为$4:5 = 12:15$、$\frac{1}{2}:\frac{1}{4} = \frac{1}{3}:\frac{1}{6}$。
(组成的比例不唯一)
(组成的比例不唯一)
4 四个小朋友各有一些零花钱,小聪有 6 元,小明有 15 元,小智有 3 元,小慧的零花钱数刚好能和其他三人的零花钱数组成一个比例,小慧可能有多少零花钱?请通过计算说明理由。
答案:
4. 解:设小慧的零花钱为$x$元。
①6和15作为比例的内项。
$3x = 6×15$ $x = 30$
②15和3作为比例的内项。
$6x = 3×15$ $x = 7.5$
③6和3作为比例的内项。
$15x = 3×6$ $x = 1.2$
答:小慧可能有30元、7.5元或1.2元零花钱。
①6和15作为比例的内项。
$3x = 6×15$ $x = 30$
②15和3作为比例的内项。
$6x = 3×15$ $x = 7.5$
③6和3作为比例的内项。
$15x = 3×6$ $x = 1.2$
答:小慧可能有30元、7.5元或1.2元零花钱。
5 一个圆的半径是 r 厘米,且 $\frac{r}{3}:\frac{8}{7}=\frac{7}{2}:\frac{r}{2}$,那么这个圆的面积是多少平方厘米?
答案:
5. 因为$\frac{8}{7}×\frac{7}{2} = \frac{r}{3}×\frac{r}{2}$,所以$r^{2} = 24$。
$3.14×24 = 75.36$(平方厘米)
答:这个圆的面积是75.36平方厘米。
解析 步骤一 $\frac{r}{3}:\frac{8}{7} = \frac{7}{2}:\frac{r}{2}$,根据比例的基本性质,可得$\frac{8}{7}×\frac{7}{2} = \frac{r}{3}×\frac{r}{2}$,即$r^{2} = 24$。
步骤二 圆的面积公式是$S = πr^{2}$,所以这个圆的面积是$3.14×24 = 75.36$(平方厘米)。
$3.14×24 = 75.36$(平方厘米)
答:这个圆的面积是75.36平方厘米。
解析 步骤一 $\frac{r}{3}:\frac{8}{7} = \frac{7}{2}:\frac{r}{2}$,根据比例的基本性质,可得$\frac{8}{7}×\frac{7}{2} = \frac{r}{3}×\frac{r}{2}$,即$r^{2} = 24$。
步骤二 圆的面积公式是$S = πr^{2}$,所以这个圆的面积是$3.14×24 = 75.36$(平方厘米)。
查看更多完整答案,请扫码查看


