第43页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
6 精挑细选。
(1)右图是一个“圆柱容球”模型,已知球与圆柱的体积之比是$$2 : 3$$,那么这个球的体积是(
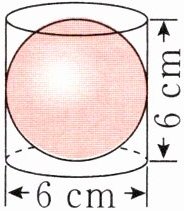
A. $$36π$B. $$54π$
C. $$81π$D. $$128π$
(2)已知$$mn = c$$,$$\frac{c}{b} = a$$,且a、b、c、m、n都是非0自然数。下面一定成立的是(
A. $$\frac{m}{n} = \frac{b}{a}$B. $$\frac{m}{n} = \frac{a}{b}$
C. $$\frac{a}{n} = \frac{b}{m}$D. $$\frac{m}{a} = \frac{b}{n}$
(1)右图是一个“圆柱容球”模型,已知球与圆柱的体积之比是$$2 : 3$$,那么这个球的体积是(
A
)立方厘米。
A. $$36π$B. $$54π$
C. $$81π$D. $$128π$
(2)已知$$mn = c$$,$$\frac{c}{b} = a$$,且a、b、c、m、n都是非0自然数。下面一定成立的是(
D
)。A. $$\frac{m}{n} = \frac{b}{a}$B. $$\frac{m}{n} = \frac{a}{b}$
C. $$\frac{a}{n} = \frac{b}{m}$D. $$\frac{m}{a} = \frac{b}{n}$
答案:
6.
(1)A
(2)D
(1)A
(2)D
7 下表是某款清洁剂浓缩液的使用方法,看表回答问题。

我已经调配了120毫升清洗陶瓷碗碟用的清洁剂,如果改为清洗水果,那么还需加入多少毫升水?
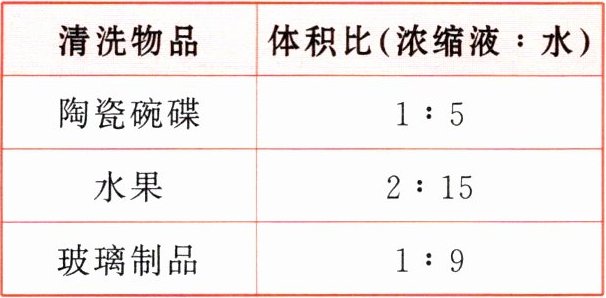

我已经调配了120毫升清洗陶瓷碗碟用的清洁剂,如果改为清洗水果,那么还需加入多少毫升水?

答案:
7. 解:设还需加入x毫升水。
$120×\frac{1}{1+5}=20$(毫升) $120-20=100$(毫升)
$2:15=20:(100+x)$
$x=50$
答:还需加入50毫升水。
$120×\frac{1}{1+5}=20$(毫升) $120-20=100$(毫升)
$2:15=20:(100+x)$
$x=50$
答:还需加入50毫升水。
8 已知甲的$$\frac{3}{5}$$和乙的$$75\%$$相等(甲、乙两数均不为0),则甲和乙的最简整数比是多少?聪聪、轩轩和梅梅都写出了等式“甲$$× \frac{3}{5} =$$乙$$× 75\%$$”,却有不同的思考。
【方法探究】请将以下三位同学的思路补充完整。

聪聪:假设算式两边的积均为1,即甲$$× \frac{3}{5} =$$乙$$× 75\% = 1$$,那么甲=(
轩轩:运用比例的基本性质,根据甲$$× \frac{3}{5} =$$乙$$× 75\%$$,可以写出比例甲:乙=(
梅梅:假设甲是10,根据甲$$× \frac{3}{5} =$$乙$$× 75\%$$,可得甲$$× \frac{3}{5} =$$(
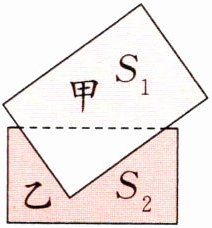
【应用迁移】如图,甲、乙两个长方形重叠在一起,甲没有重叠部分的面积为$$S_1$$,相当于甲面积的$$\frac{3}{5}$$;乙没有重叠部分的面积是$$S_2$$,相当于乙面积的$$\frac{4}{9}$$。甲、乙的面积比是(
【方法探究】请将以下三位同学的思路补充完整。

聪聪:假设算式两边的积均为1,即甲$$× \frac{3}{5} =$$乙$$× 75\% = 1$$,那么甲=(
$\frac{5}{3}$
),乙=($\frac{4}{3}$
),甲:乙=($\frac{5}{3}$
):($\frac{4}{3}$
),化简后是(5
):(4
)。轩轩:运用比例的基本性质,根据甲$$× \frac{3}{5} =$$乙$$× 75\%$$,可以写出比例甲:乙=(
75%
):($\frac{3}{5}$
),化简后是(5
):(4
)。梅梅:假设甲是10,根据甲$$× \frac{3}{5} =$$乙$$× 75\%$$,可得甲$$× \frac{3}{5} =$$(
6
),乙=(8
),所以甲:乙$$= 10 :$$(8
),化简后是(5
):(4
)。【应用迁移】如图,甲、乙两个长方形重叠在一起,甲没有重叠部分的面积为$$S_1$$,相当于甲面积的$$\frac{3}{5}$$;乙没有重叠部分的面积是$$S_2$$,相当于乙面积的$$\frac{4}{9}$$。甲、乙的面积比是(
25
):(18
)。
答案:
8. 【方法探究】$\frac{5}{3}$ $\frac{4}{3}$ $\frac{5}{3}$ $\frac{4}{3}$ 5 4
75% $\frac{3}{5}$ 5 4 6 8 8 5 4
【应用迁移】25 18
解析
●方法探究:按照三位同学的思路分别填空即可。
●应用迁移:通过计算重叠部分的面积作答。
步骤一 重叠部分的面积=甲的面积-$S_{1}=$甲的面积$×(1-\frac{3}{5})$,且重叠部分的面积=乙的面积$-S_{2}=$乙的面积$×(1-\frac{4}{9})$。
步骤二 甲的面积$×(1-\frac{3}{5})=$乙的面积$×(1-\frac{4}{9})$,即甲的面积$×\frac{2}{5}=$乙的面积$×\frac{5}{9}$,甲、乙的面积比为$\frac{5}{9}:\frac{2}{5}=25:18$。
75% $\frac{3}{5}$ 5 4 6 8 8 5 4
【应用迁移】25 18
解析
●方法探究:按照三位同学的思路分别填空即可。
●应用迁移:通过计算重叠部分的面积作答。
步骤一 重叠部分的面积=甲的面积-$S_{1}=$甲的面积$×(1-\frac{3}{5})$,且重叠部分的面积=乙的面积$-S_{2}=$乙的面积$×(1-\frac{4}{9})$。
步骤二 甲的面积$×(1-\frac{3}{5})=$乙的面积$×(1-\frac{4}{9})$,即甲的面积$×\frac{2}{5}=$乙的面积$×\frac{5}{9}$,甲、乙的面积比为$\frac{5}{9}:\frac{2}{5}=25:18$。
查看更多完整答案,请扫码查看


