《2025年步步高精准讲练物理选择性必修第二册》

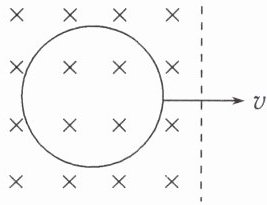
如图所示，将一个闭合金属圆环从有界匀强磁场中匀速拉出，第一次速度为 $ v $，通过金属圆环某一横截面的电荷量为 $ q_1 $，第二次速度为 $ 2v $，通过金属圆环某一横截面的电荷量为 $ q_2 $，则 $ q_1 : q_2 = $1:1；若将金属圆环由原位置翻转 $ 180° $（圆环面积为 $ S $，总电阻为 $ R $，匀强磁场磁感应强度为 $ B $），此过程中通过圆环横截面的电荷量为____$\frac{2BS}{R}$。

答案： 1:1；$\frac{2BS}{R}$（或 $ \frac{2BS}{R} $）。
（以填空形式，答案为：
$ q_1 : q_2 = 1:1 $；
通过圆环横截面的电荷量为 $ \frac{2BS}{R} $。）

例 2
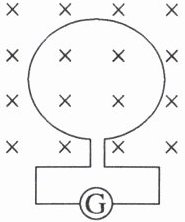
物理实验中，常用一种叫作“冲击电流计”的仪器测定通过电路的电荷量，如图所示，探测线圈与冲击电流计串联后可用来测定磁场的磁感应强度。已知线圈的匝数为 $ n $，面积为 $ S $，线圈与冲击电流计组成的回路电阻为 $ R $。若将线圈放在被测匀强磁场中，开始时线圈平面与磁场垂直，现把探测线圈翻转 $ 180° $，冲击电流计测出通过线圈的电荷量为 $ q $，由上述数据可测出被测磁场的磁感应强度为（C）

A.$ \frac{qR}{S} $
B.$ \frac{qR}{nS} $
C.$ \frac{qR}{2nS} $
D.$ \frac{qR}{2S} $

答案： C　[q = $\bar{I}$·$\Delta t$ = $\frac{\bar{E}}{R}$·$\Delta t$ = n$\frac{\Delta\Phi}{R\Delta t}$·$\Delta t$ = n$\frac{\Delta\Phi}{R}$ = n$\frac{2BS}{R}$，所以B = $\frac{qR}{2nS}$，C正确。]

例 3
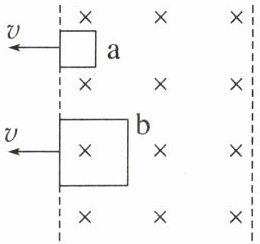
如图所示，用粗细相同的铜丝做成边长分别为 $ d $ 和 $ 2d $ 的单匝闭合线框 $ a $ 和 $ b $，以相同的速度将线框从磁感应强度为 $ B $ 的匀强磁场区域中匀速地拉到磁场外。若此过程中通过两线框某一横截面的电荷量分别为 $ q_a $、$ q_b $，则 $ q_a : q_b $ 为（B）

A.$ 1 : 4 $
B.$ 1 : 2 $
C.$ 1 : 1 $
D.不能确定

答案： B　[设闭合线框的边长为L，则通过线框某一横截面的电荷量为q = $\bar{I}$$\Delta t$ = $\frac{\bar{E}}{R}$$\Delta t$ = $\frac{\Delta\Phi}{R\Delta t}$$\Delta t$ = $\frac{B·\Delta S}{R}$ = $\frac{BL^2}{R}$，R = ρ$\frac{4L}{S_横}$，则q = $\frac{BS_横L}{4\rho}$，则$\frac{q_a}{q_b}$ = $\frac{L_a}{L_b}$ = $\frac{d}{2d}$ = $\frac{1}{2}$，故选B。]

例 4
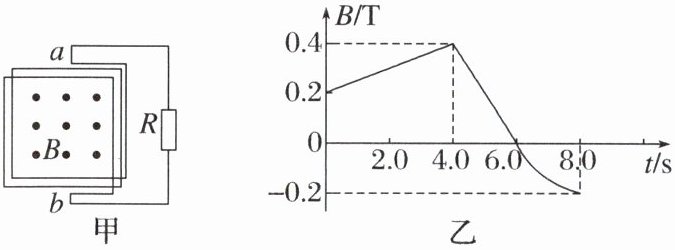
（2024·杭州市第十四中学高二期中）如图甲所示，在一个正方形金属线圈区域内存在匀强磁场，磁场的方向与线圈平面垂直。金属线圈所围的面积 $ S = 200 \, cm^2 $，匝数 $ n = 1000 $，线圈电阻的阻值为 $ r = 2.0 \, \Omega $。线圈与阻值 $ R = 8.0 \, \Omega $ 的定值电阻构成闭合回路。匀强磁场的磁感应强度随时间变化的情况如图乙所示，$ 6.0 \sim 8.0 \, s $ 时间内图线为曲线，其余时间内图线为直线。求：

1. $ t_1 = 2.0 \, s $ 时通过线圈的磁通量；
2. $ t_1 = 2.0 \, s $ 时通过电阻 $ R $ 的感应电流的大小和方向；
3. $ t_2 = 5.0 \, s $ 时刻，线圈端点 $ a $、$ b $ 间的电压；
4. 在 $ 4.0 \sim 8.0 \, s $ 时间内通过电阻 $ R $ 的电荷量。

答案：
1. 6.0×10⁻³Wb　2. 0.1A 方向向上　3. 3.2V　4. 1.2C
解析　
(1)t₁ = 2.0s时通过线圈的磁通量Φ = BS = 0.3×200×10⁻⁴Wb = 6.0×10⁻³Wb。
(2)t₁ = 2.0s时感应电动势E = n$\frac{\Delta B}{\Delta t}$S = 1000×$\frac{0.4 - 0.2}{4.0}$×200×10⁻⁴V = 1V，通过R的感应电流的大小I = $\frac{E}{R + r}$ = $\frac{1}{8.0 + 2.0}$A = 0.1A，根据楞次定律可知，通过R的电流方向向上。
(3)t₂ = 5.0s时刻，感应电动势E' = n$\frac{\Delta B'}{\Delta t}$S = 1000×$\frac{0.4 - 0}{6.0 - 4.0}$×200×10⁻⁴V = 4V，根据楞次定律可知a端电势高，则线圈端点a、b间的电压U_ab = $\frac{E'R}{R + r}$ = $\frac{4×8.0}{8.0 + 2.0}$V = 3.2V。
(4)在4.0～8.0s时间内通过电阻R的电荷量q = $\frac{\bar{E}}{R + r}$$\Delta t$ = $\frac{n\Delta\Phi}{R + r}$ = $\frac{n\Delta B·S}{R + r}$ = 1000×$\frac{0.4 + 0.2}{8.0 + 2.0}$×200×10⁻⁴C = 1.2C。