第4页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
20. (12 分)如图,用同样规格的黑、灰两色的正方形瓷砖铺设矩形地面,请观察下列图形并解答有关问题。
(1)在第 $n$ 个图形中,共有瓷砖
(2)按上述铺设方案,铺一块这样的矩形地面共用了 $506$ 块瓷砖,求此时 $n$ 的值。
(3)黑瓷砖每块 $4$ 元,灰瓷砖每块 $3$ 元,则问题(2)中,共花多少元购买瓷砖?

(1)在第 $n$ 个图形中,共有瓷砖
$(n^{2}+5n + 6)$
块,其中灰色瓷砖$(n^{2}+n)$
块,黑色瓷砖$(4n + 6)$
块(均用含 $n$ 的代数式表示)。(2)按上述铺设方案,铺一块这样的矩形地面共用了 $506$ 块瓷砖,求此时 $n$ 的值。
(3)黑瓷砖每块 $4$ 元,灰瓷砖每块 $3$ 元,则问题(2)中,共花多少元购买瓷砖?

答案:
20.解:
(1)$(n^{2}+5n + 6)$ $(n^{2}+n)$ $(4n + 6)$
(2)由题意得$n^{2}+5n + 6 = 506$, 解得$n = 20$或$n = -25$(不合题意,舍去).
(3)灰瓷砖块数是$n^{2}+n = 20^{2}+20 = 420$, 黑瓷砖块数是$506 - 420 = 86$, 则共需$86×4 + 420×3 = 1604$(元). 答:共花1604元钱购买瓷砖.
(1)$(n^{2}+5n + 6)$ $(n^{2}+n)$ $(4n + 6)$
(2)由题意得$n^{2}+5n + 6 = 506$, 解得$n = 20$或$n = -25$(不合题意,舍去).
(3)灰瓷砖块数是$n^{2}+n = 20^{2}+20 = 420$, 黑瓷砖块数是$506 - 420 = 86$, 则共需$86×4 + 420×3 = 1604$(元). 答:共花1604元钱购买瓷砖.
21. (14 分)阅读材料:
用“转化”的数学思想,我们可以解一些新的方程。例如,一元三次方程 $x^{3}+x^{2}-2x = 0$,可以通过因式分解把它转化为 $x(x^{2}+x - 2)=0$,解方程 $x = 0$ 和 $x^{2}+x - 2 = 0$,可得方程 $x^{3}+x^{2}-2x = 0$ 的解。
(1)问题:方程 $x^{3}+x^{2}-2x = 0$ 的解是 $x_{1}=0$,$x_{2}=$
(2)拓展:用“转化”思想求方程 $\sqrt{2x + 3}=x$ 的解。
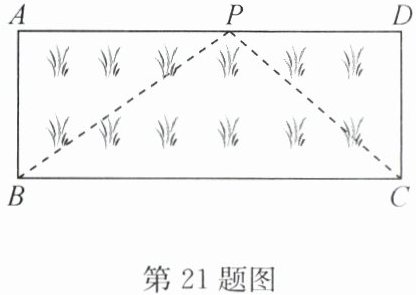
(3)应用:如图,已知矩形草坪 $ABCD$ 的长 $AD = 8$ m,宽 $AB = 3$ m,小华把一根长为 $10$ m 的绳子的一端固定在点 $B$,沿草坪边 $BA$,$AP$ 走到点 $P$ 处,把长绳 $PB$ 段拉直并固定在点 $P$,然后沿草坪边 $PD$,$DC$ 走到点 $C$ 处,把长绳剩下的一段拉直,长绳的另一端恰好落在点 $C$ 处。求 $AP$ 的长。
用“转化”的数学思想,我们可以解一些新的方程。例如,一元三次方程 $x^{3}+x^{2}-2x = 0$,可以通过因式分解把它转化为 $x(x^{2}+x - 2)=0$,解方程 $x = 0$ 和 $x^{2}+x - 2 = 0$,可得方程 $x^{3}+x^{2}-2x = 0$ 的解。
(1)问题:方程 $x^{3}+x^{2}-2x = 0$ 的解是 $x_{1}=0$,$x_{2}=$
$-2$
,$x_{3}=$$1$
。(2)拓展:用“转化”思想求方程 $\sqrt{2x + 3}=x$ 的解。
(3)应用:如图,已知矩形草坪 $ABCD$ 的长 $AD = 8$ m,宽 $AB = 3$ m,小华把一根长为 $10$ m 的绳子的一端固定在点 $B$,沿草坪边 $BA$,$AP$ 走到点 $P$ 处,把长绳 $PB$ 段拉直并固定在点 $P$,然后沿草坪边 $PD$,$DC$ 走到点 $C$ 处,把长绳剩下的一段拉直,长绳的另一端恰好落在点 $C$ 处。求 $AP$ 的长。

答案:
21.解:
(1)$\because x^{3}+x^{2}-2x = 0$,$x(x^{2}+x - 2)=0$, $x(x + 2)(x - 1)=0$,$\therefore x = 0$或$x + 2 = 0$或$x - 1 = 0$, $\therefore x_{1}=0$,$x_{2}=-2$,$x_{3}=1$.故答案为$-2$,$1$.
(2)方程的两边平方,得$2x + 3 = x^{2}$,即$x^{2}-2x - 3 = 0$, $\therefore (x - 3)(x + 1)=0$,$x - 3 = 0$或$x + 1 = 0$, $\therefore x_{1}=3$,$x_{2}=-1$, 当$x = -1$时,$\sqrt{2x + 3}=\sqrt{1}=1\neq -1$,$\therefore -1$不是原方程 的解, $\therefore$方程$\sqrt{2x + 3}=x$的解是$x = 3$.
(3)设$AP = x$m,则$PD=(8 - x)$m,$\because$四边形$ABCD$是矩形, $\therefore\angle A=\angle D = 90^{\circ}$,$AB = CD = 3$m. $\because BP + CP = 10$m,$BP=\sqrt{AB^{2}+AP^{2}}$,$CP=\sqrt{PD^{2}+CD^{2}}$, $\therefore\sqrt{9 + x^{2}}+\sqrt{(8 - x)^{2}+9}=10$, $\therefore\sqrt{(8 - x)^{2}+9}=10-\sqrt{9 + x^{2}}$, 两边平方,得$(8 - x)^{2}+9 = 100 - 20\sqrt{9 + x^{2}}+9 + x^{2}$. 整理,得$5\sqrt{x^{2}+9}=4x + 9$, 两边平方并整理,得$x^{2}-8x + 16 = 0$, 即$(x - 4)^{2}=0$,$\therefore x = 4$.经检验,$x = 4$是方程的解. 答:$AP$的长为4m.
(1)$\because x^{3}+x^{2}-2x = 0$,$x(x^{2}+x - 2)=0$, $x(x + 2)(x - 1)=0$,$\therefore x = 0$或$x + 2 = 0$或$x - 1 = 0$, $\therefore x_{1}=0$,$x_{2}=-2$,$x_{3}=1$.故答案为$-2$,$1$.
(2)方程的两边平方,得$2x + 3 = x^{2}$,即$x^{2}-2x - 3 = 0$, $\therefore (x - 3)(x + 1)=0$,$x - 3 = 0$或$x + 1 = 0$, $\therefore x_{1}=3$,$x_{2}=-1$, 当$x = -1$时,$\sqrt{2x + 3}=\sqrt{1}=1\neq -1$,$\therefore -1$不是原方程 的解, $\therefore$方程$\sqrt{2x + 3}=x$的解是$x = 3$.
(3)设$AP = x$m,则$PD=(8 - x)$m,$\because$四边形$ABCD$是矩形, $\therefore\angle A=\angle D = 90^{\circ}$,$AB = CD = 3$m. $\because BP + CP = 10$m,$BP=\sqrt{AB^{2}+AP^{2}}$,$CP=\sqrt{PD^{2}+CD^{2}}$, $\therefore\sqrt{9 + x^{2}}+\sqrt{(8 - x)^{2}+9}=10$, $\therefore\sqrt{(8 - x)^{2}+9}=10-\sqrt{9 + x^{2}}$, 两边平方,得$(8 - x)^{2}+9 = 100 - 20\sqrt{9 + x^{2}}+9 + x^{2}$. 整理,得$5\sqrt{x^{2}+9}=4x + 9$, 两边平方并整理,得$x^{2}-8x + 16 = 0$, 即$(x - 4)^{2}=0$,$\therefore x = 4$.经检验,$x = 4$是方程的解. 答:$AP$的长为4m.
查看更多完整答案,请扫码查看


