《2025年新目标检测同步单元测试卷九年级数学上册人教版》

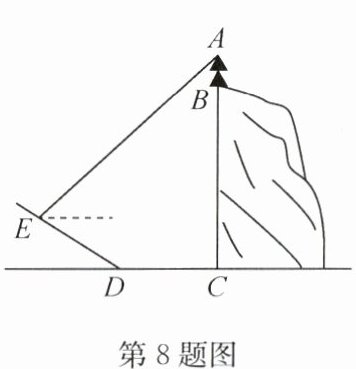
8. 如图，垂直于水平面的 5G 信号塔 $ AB $ 建在垂直于水平面的悬崖边 $ B $ 点处，某测量员从山脚 $ C $ 点出发沿水平方向前行 78 米到 $ D $ 点(点 $ A,B,C $ 在同一直线上)，再沿斜坡 $ DE $ 方向前行 78 米到 $ E $ 点(点 $ A,B,C,D,E $ 在同一平面内)，在点 $ E $ 处测得 5G 信号塔顶端 $ A $ 的仰角为 $ 43^{\circ} $，悬崖 $ BC $ 的高为 144.5 米，斜坡 $ DE $ 的坡度(或坡比)$ i = 1:2.4 $，则信号塔 $ AB $ 的高度约为(D)
(参考数据：$ \sin 43^{\circ} \approx 0.68 $，$ \cos 43^{\circ} \approx 0.73 $，$ \tan 43^{\circ} \approx 0.93 $)

A.23 米
B.24 米
C.24.5 米
D.25 米

答案：
8.D 解析：如图,过点$E$作$EF \perp CD$交$CD$的延长线于点$F$,过点$E$作$EM \perp AC$于点$M$. $\because$斜坡$DE$的坡度(或坡比)$i = 1:2.4$, $DE = CD = 78$米, $\therefore$设$EF = x$米,则$DF = 2.4x$米. 在$\text{Rt} \triangle DEF$中, $EF^2 + DF^2 = DE^2$,即$x^2 + (2.4x)^2 = 78^2$,解得$x = 30$, $\therefore EF = 30$米, $DF = 72$米, $\therefore CF = DF + DC = 72 + 78 = 150$(米). $\because EM \perp AC$, $AC \perp CD$, $EF \perp CD$, $\therefore$四边形$EFCM$是矩形, $\therefore EM = CF = 150$米, $CM = EF = 30$米. 在$\text{Rt} \triangle AEM$中, $\because \angle AEM = 43^\circ$, $\therefore AM = EM \cdot \tan 43^\circ \approx 150 \times 0.93 = 139.5$(米), $\therefore AC = AM + CM = 139.5 + 30 = 169.5$(米), $\therefore AB = AC - BC = 169.5 - 144.5 = 25$(米).故选D.

9. 在 $ \triangle ABC $ 中，$ \angle A,\angle B,\angle C $ 所对的边分别是 $ a,b,c $，$ \angle A = 90^{\circ} $，若 $ \tan B = \frac{4}{3} $，$ c = 6 $，则 $ a $ 的值为10。

答案： 9.10 解析：$\because \angle A = 90^\circ$, $\tan B = \frac{4}{3}$, $\therefore \frac{b}{c} = \frac{4}{3}$. $\because c = 6$, $\therefore b = 8$, $\therefore a = \sqrt{6^2 + 8^2} = 10$.

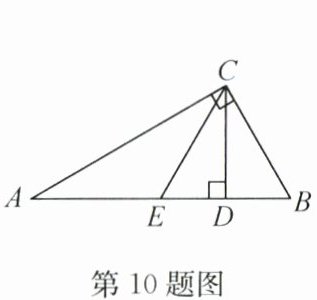
10. 如图，在 $ Rt \triangle ABC $ 中，$ \angle ACB = 90^{\circ} $，$ \angle A = 30^{\circ} $，$ AB = 4 $，$ CD \perp AB $ 于点 $ D $，$ E $ 是 $ AB $ 的中点，则 $ DE $ 的长为1。

答案： 10.1　解析:
∵∠ACB=90°,∠A=30°,
∴∠B=60°,
　在Rt△ACB中，
∵∠A=30°,AB=4,
∴BC=2,
　又
∵E是AB的中点，
∴EB=2,
　在△CBE中,∠B=60°,EB=CB=2,
∴△CBE是等边三角形，又
∵CD⊥DB,
∴ED=$\frac{1}{2}$EB=1.

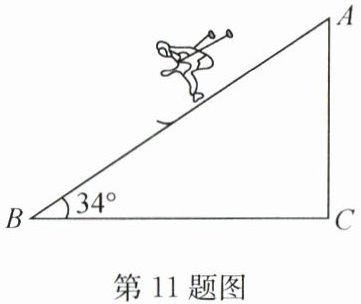
11. 如图，一名滑雪运动员沿着倾斜角为 $ 34^{\circ} $ 的斜坡，从 $ A $ 滑行至 $ B $。已知 $ AB = 500 $ 米，则这名滑雪运动员的高度下降了约280米。(参考数据：$ \sin 34^{\circ} \approx 0.56 $，$ \cos 34^{\circ} \approx 0.83 $，$ \tan 34^{\circ} \approx 0.67 $)

答案： 11.280

12. 如果方程 $ x^{2} - 7x + 12 = 0 $ 的两个根分别是 $ Rt \triangle ABC $ 的两条边长，$ \triangle ABC $ 中最小的角为 $ \angle A $，那么 $ \tan A $ 的值为$\frac{\sqrt{7}}{3}$或$\frac{3}{4}$。

答案： 12.$\frac{\sqrt{7}}{3}$或$\frac{3}{4}$　解析:解方程x²−7x+12=0,得x₁=3,x₂=4.若
3、4为直角边长，则tanA=$\frac{3}{4}$;若4为斜边长，则另一条直角边长为$\sqrt{7}$,tanA=$\frac{\sqrt{7}}{3}$.

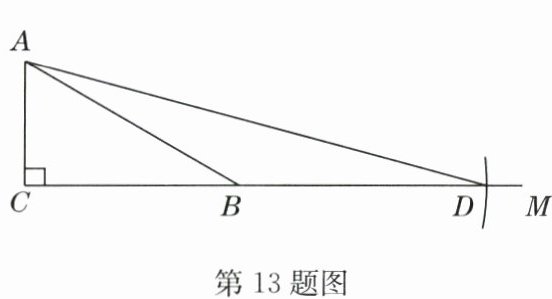
13. 如何求 $ \tan 75^{\circ} $ 的值？按下面的方法作图可解决问题，如图，在 $ Rt \triangle ABC $ 中，$ AC = k $，$ \angle ACB = 90^{\circ} $，$ \angle ABC = 30^{\circ} $，延长 $ CB $ 至点 $ M $，在射线 $ BM $ 上截取线段 $ BD $，使 $ BD = AB $，连接 $ AD $，依据此图可求得 $ \tan 75^{\circ} $ 的值为2+ $\sqrt{3}$。

答案： 13.2+ $\sqrt{3}$　解析:在Rt△ABC中,AC=k,∠ACB=90°,∠ABC =30°,
∴AB=BD=2k,∠BAD=∠BDA=15°,BC=$\sqrt{3}$k,
∴∠CAD=∠CAB+∠BAD=75°,CD=CB+BD=$\sqrt{3}$k+2k,
∴在Rt△ACD中,tan75°=tan∠CAD=$\frac{CD}{AC}$=$\frac{\sqrt{3}k + 2k}{k}$=2+$\sqrt{3}$.