第16页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
19. (14 分)某商贸公司购进某种商品的成本为 $ 20 $ 元/kg,经过市场调研发现,这种商品在未来 $ 40 $ 天的销售单价 $ y $(元/kg)与时间 $ x $(天)之间的函数关系式为
$ y = \begin{cases} 0.25x + 30(1 \leq x \leq 20), \\ 35(20 < x \leq 40), \end{cases} $
$ x $ 为整数,且日销量 $ m $(kg)与时间 $ x $(天)之间的变化规律符合一次函数关系,如下表:

(1)$ m $ 与 $ x $ 的函数关系为
(2)哪一天的销售利润最大?最大日销售利润是多少?
(3)在实际销售的前 $ 20 $ 天中,公司决定每销售 $ 1kg $ 商品就捐赠 $ n $ 元利润($ n < 4 $)给当地福利院,之后发现:在前 $ 20 $ 天中,每天扣除捐赠后的日销售利润随时间 $ x $ 的增大而增大,求 $ n $ 的取值范围。
$ y = \begin{cases} 0.25x + 30(1 \leq x \leq 20), \\ 35(20 < x \leq 40), \end{cases} $
$ x $ 为整数,且日销量 $ m $(kg)与时间 $ x $(天)之间的变化规律符合一次函数关系,如下表:

(1)$ m $ 与 $ x $ 的函数关系为
m=-2x+144(x≥1)
。(2)哪一天的销售利润最大?最大日销售利润是多少?
(3)在实际销售的前 $ 20 $ 天中,公司决定每销售 $ 1kg $ 商品就捐赠 $ n $ 元利润($ n < 4 $)给当地福利院,之后发现:在前 $ 20 $ 天中,每天扣除捐赠后的日销售利润随时间 $ x $ 的增大而增大,求 $ n $ 的取值范围。
答案:
19.解:
(1)设m=kx+b,将(1,142),(3,138)代入可得
$\begin{cases}142 = k + b, \\138 = 3k + b.\end{cases}$
解得$\begin{cases}k = -2, \\b = 144,\end{cases}$
∴m=-2x+144(x≥1).
(2)当1≤x≤20时,销售利润W=my-20m=(-2x+144)·(0.25x+30-20)=-$\frac{1}{2}$(x-16)²+1568,
当x=16时,销售利润最大,为1568元;
当20<x≤40时,销售利润W=my-20m=-30x+2160,
当x=21时,销售利润最大,为1530元.
综上所述,第16天销售利润最大,为1568元.
(3)在前20天中,每天扣除捐赠后的日销售利润为:
W'=my-20m-nm=(0.25x+30-20-n)(-2x+144)=-$\frac{1}{2}$x²+(16+2n)x+1440-144n,
∵在前20天中,每天扣除捐赠后的日销售利润随时间x的增大而增大,且x只能取整数,故只要第20天的利润高于第19天,即对称轴在直线x=19.5右侧,
∴16+2n>19.5,
∴n>1.75,又
∵n<4,
∴n的取值范围是1.75<n<4.
(1)设m=kx+b,将(1,142),(3,138)代入可得
$\begin{cases}142 = k + b, \\138 = 3k + b.\end{cases}$
解得$\begin{cases}k = -2, \\b = 144,\end{cases}$
∴m=-2x+144(x≥1).
(2)当1≤x≤20时,销售利润W=my-20m=(-2x+144)·(0.25x+30-20)=-$\frac{1}{2}$(x-16)²+1568,
当x=16时,销售利润最大,为1568元;
当20<x≤40时,销售利润W=my-20m=-30x+2160,
当x=21时,销售利润最大,为1530元.
综上所述,第16天销售利润最大,为1568元.
(3)在前20天中,每天扣除捐赠后的日销售利润为:
W'=my-20m-nm=(0.25x+30-20-n)(-2x+144)=-$\frac{1}{2}$x²+(16+2n)x+1440-144n,
∵在前20天中,每天扣除捐赠后的日销售利润随时间x的增大而增大,且x只能取整数,故只要第20天的利润高于第19天,即对称轴在直线x=19.5右侧,
∴16+2n>19.5,
∴n>1.75,又
∵n<4,
∴n的取值范围是1.75<n<4.
20. (16 分)如图①,已知二次函数 $ y = ax^2 + bx + c(a \neq 0) $ 的图象与 $ x $ 轴交于点 $ A(1, 0) $、点 $ C $,与 $ y $ 轴交于点 $ B(0, 3) $,对称轴是直线 $ x = -1 $,顶点是 $ M $。
(1)求二次函数的解析式。
(2)点 $ P $ 是抛物线上的动点,点 $ D $ 是对称轴上的动点,当以 $ P $、$ D $、$ B $、$ C $ 为顶点的四边形是平行四边形时,求点 $ D $ 的坐标。
(3)如图②,过原点的直线 $ l $ 平分 $ \triangle MBC $ 的面积,求直线 $ l $ 的解析式。
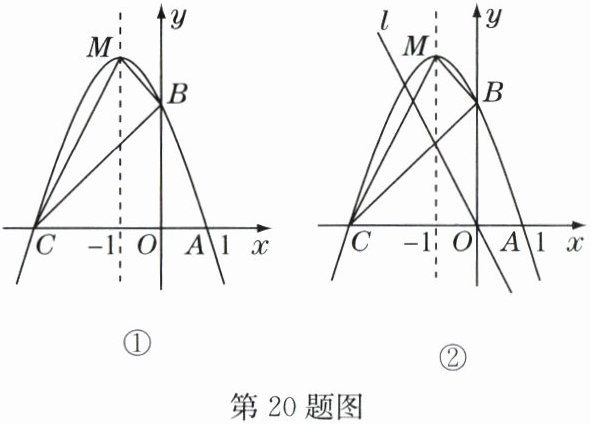
(1)求二次函数的解析式。
(2)点 $ P $ 是抛物线上的动点,点 $ D $ 是对称轴上的动点,当以 $ P $、$ D $、$ B $、$ C $ 为顶点的四边形是平行四边形时,求点 $ D $ 的坐标。
(3)如图②,过原点的直线 $ l $ 平分 $ \triangle MBC $ 的面积,求直线 $ l $ 的解析式。

答案:
20.解:
(1)
∵二次函数y=ax²+bx+c(a≠0)的图象与x轴交于点A(1,0)、点C,对称轴为直线x=-1,
∴点C的坐标为(-3,0).
设二次函数解析式为y=a(x-1)(x+3),把点B(0,3)代入得a=-1,
∴二次函数的解析式为y=-(x-1)(x+3)=-x²-2x+3.
(2)如图①.
当D₁(-1,0),P₁(-2,3)时,
∵P₁B=CD₁,P₁B//CD₁,
∴四边形CD₁BP₁为平行四边形.
当BC//D₂P₂,BC=P₂D₂时,四边形BCP₂D₂是平行四边形.
∵BO=CO=3,
∴P₂D₂=BC=3$\sqrt{2}$.
设D₂(-1,m),则P₂(-4,m-3),把P₂的坐标代入抛物线的解析式,得m-3=-16+8+3,所以m=-2,
∴D₂(-1,-2).
当D₃P₃//BC,D₃P₃=BC时,四边形BCD₃P₃是平行四边形.
设D₃(-1,n),则P₃(2,n+3).
把点P₃的坐标代入抛物线的解析式,得n+3=-4-4+3,所以n=-8,
∴D₃(-1,-8).
综上所述,点D的坐标为(-1,0)或(-1,-2)或(-1,-8).
(3)连接OM,如图②,由二次函数解析式知,点M的坐标为(-1,4).
∵C(-3,0),B(0,3),
∴S△MBC=S△MCO+S△MBO-S△COB=$\frac{1}{2}$×3×4+$\frac{1}{2}$×3×1-$\frac{1}{2}$×3×3=3.
设直线l的解析式为y=kx(k≠0).
易求得直线BC的解析式为y=x+3,直线CM的解析式为y=2x+6.
由$\begin{cases}y = kx, \\y = x + 3\end{cases}$
解得$\begin{cases}x = \frac{3}{k - 1}, \\y = \frac{3k}{k - 1}\end{cases}$
∴点N($\frac{3}{k - 1}$, $\frac{3k}{k - 1}$).
由$\begin{cases}y = kx, \\y = 2x + 6\end{cases}$
解得$\begin{cases}x = \frac{6}{k - 2}, \\y = \frac{6k}{k - 2}\end{cases}$
∴点Q($\frac{6}{k - 2}$, $\frac{6k}{k - 2}$).
∵S△CNQ=$\frac{3}{2}$,
∴S△COQ-S△CON=$\frac{3}{2}$,
∴$\frac{1}{2}$×3×$\frac{6k}{k - 2}$-$\frac{1}{2}$×3×$\frac{3k}{k - 1}$=$\frac{3}{2}$,
∴k=-2(k=$\frac{1}{2}$不合题意,舍去),
∴直线l的解析式为y=-2x.

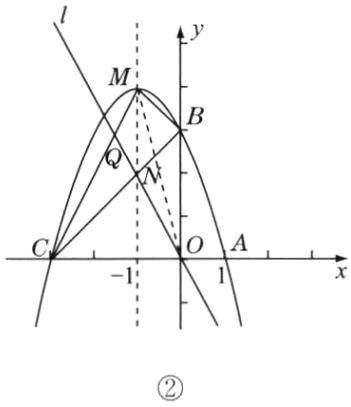
20.解:
(1)
∵二次函数y=ax²+bx+c(a≠0)的图象与x轴交于点A(1,0)、点C,对称轴为直线x=-1,
∴点C的坐标为(-3,0).
设二次函数解析式为y=a(x-1)(x+3),把点B(0,3)代入得a=-1,
∴二次函数的解析式为y=-(x-1)(x+3)=-x²-2x+3.
(2)如图①.
当D₁(-1,0),P₁(-2,3)时,
∵P₁B=CD₁,P₁B//CD₁,
∴四边形CD₁BP₁为平行四边形.
当BC//D₂P₂,BC=P₂D₂时,四边形BCP₂D₂是平行四边形.
∵BO=CO=3,
∴P₂D₂=BC=3$\sqrt{2}$.
设D₂(-1,m),则P₂(-4,m-3),把P₂的坐标代入抛物线的解析式,得m-3=-16+8+3,所以m=-2,
∴D₂(-1,-2).
当D₃P₃//BC,D₃P₃=BC时,四边形BCD₃P₃是平行四边形.
设D₃(-1,n),则P₃(2,n+3).
把点P₃的坐标代入抛物线的解析式,得n+3=-4-4+3,所以n=-8,
∴D₃(-1,-8).
综上所述,点D的坐标为(-1,0)或(-1,-2)或(-1,-8).
(3)连接OM,如图②,由二次函数解析式知,点M的坐标为(-1,4).
∵C(-3,0),B(0,3),
∴S△MBC=S△MCO+S△MBO-S△COB=$\frac{1}{2}$×3×4+$\frac{1}{2}$×3×1-$\frac{1}{2}$×3×3=3.
设直线l的解析式为y=kx(k≠0).
易求得直线BC的解析式为y=x+3,直线CM的解析式为y=2x+6.
由$\begin{cases}y = kx, \\y = x + 3\end{cases}$
解得$\begin{cases}x = \frac{3}{k - 1}, \\y = \frac{3k}{k - 1}\end{cases}$
∴点N($\frac{3}{k - 1}$, $\frac{3k}{k - 1}$).
由$\begin{cases}y = kx, \\y = 2x + 6\end{cases}$
解得$\begin{cases}x = \frac{6}{k - 2}, \\y = \frac{6k}{k - 2}\end{cases}$
∴点Q($\frac{6}{k - 2}$, $\frac{6k}{k - 2}$).
∵S△CNQ=$\frac{3}{2}$,
∴S△COQ-S△CON=$\frac{3}{2}$,
∴$\frac{1}{2}$×3×$\frac{6k}{k - 2}$-$\frac{1}{2}$×3×$\frac{3k}{k - 1}$=$\frac{3}{2}$,
∴k=-2(k=$\frac{1}{2}$不合题意,舍去),
∴直线l的解析式为y=-2x.


查看更多完整答案,请扫码查看


