《2025年新目标检测同步单元测试卷九年级数学上册人教版》

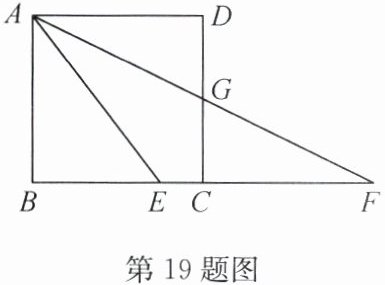
19. （12分）如图，点 $E$ 是正方形 $ABCD$ 的边 $BC$ 上一点，连接 $AE$，将线段 $AE$ 绕点 $E$ 顺时针旋转一定的角度得到 $EF$，点 $C$ 在 $EF$ 上，连接 $AF$ 交边 $CD$ 于点 $G$.
（1）若 $AB = 4$，$BF = 8$，求 $EC$ 的长.
（2）求证：$AE = BE + DG$.

答案：
19.
(1)解:设AE=EF=x,
∵四边形ABCD是正方形，
∴∠ABE =90°,AB=BC=4.
∵BF=8,
∴CF=8 - 4=4,BE=BF - EF=8 - x,在Rt△ABE中,AB=4,AE=x,
∴x²=4²+(8 - x)²,解得x=5,
∴EC=EF - CF=1.
(2)证明:如图，延长EB到点H,使得BH=DG,易证△ADG ≌△ABH(SAS),
∴∠BAH=∠DAG,
∴∠HAF=∠BAD=90°.
∵AE=EF,
∴∠EAF=∠F.
∵∠EAH+∠EAF=90°,∠F+∠H=90°,
∴∠H=∠EAH,
∴EA=EH;
∵EH=BE +BH=BE+DG,
∴AE=BE+DG.

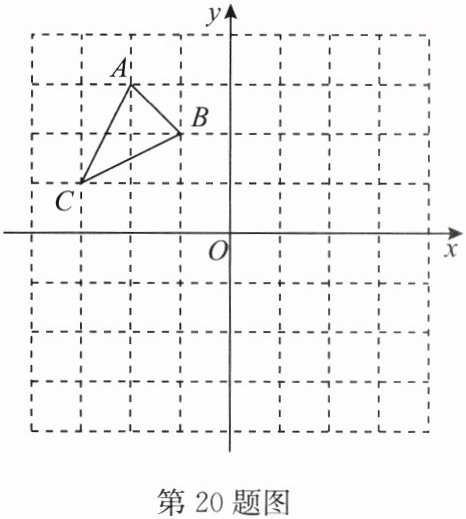
20. (12分)如图，在边长均为1的正方形组成的网格中，$\triangle ABC$ 的顶点均在格点上，点 $A$，$B$，$C$ 的坐标分别是 $A(-2,3)$，$B(-1,2)$，$C(-3,1)$，$\triangle ABC$ 绕点 $O$ 顺时针旋转 $90°$ 后得到 $\triangle A_1B_1C_1$.
(1)在正方形网格中作出 $\triangle A_1B_1C_1$；
(2)在旋转过程中，点 $A$ 经过的路径 $\overset{\frown}{AA_1}$ 的长度为$\frac{\sqrt{13}}{2}\pi$；
(3)在 $y$ 轴上找一点 $D$，使 $DB + DB_1$ 的值最小，并求出 $D$ 点的坐标.

答案：
20.解:
(1)如图所示.

(2)连接OA,OA₁,则OA₁=OA=√13,∠AOA₁=90°,在旋转过程中,点A经过的路径AA₁的长度为90×π×√13/180=√13/2π.
(3)连接BB₁交y轴于点D,设D′为y轴上异于点D的点，显然D′B+D′B₁＞DB+DB₁,
∴当点D是BB₁与y轴的交点时，DB+DB₁的值最小.设直线BB₁的解析式为y=kx + b,依据题意可得
{-k + b=2,
{2k + b=1,
解得{k=-1/3,
{b=5/3.
∴直线BB₁的解析式为y=-1/3x + 5/3,
∴D(0,5/3).

21. （14分）如图①，在 $\triangle ABC$ 中，$\angle A = 36°$，$AB = AC$，$\angle ABC$ 的平分线 $BE$ 交 $AC$ 于点 $E$.
（1）求证：$AE = BC$.
（2）如图②，过点 $E$ 作 $EF // CB$ 交 $AB$ 于点 $F$，将 $\triangle AEF$ 绕点 $A$ 逆时针旋转 $\angle \alpha(0° ＜ \angle \alpha ＜ 144°)$ 得到 $\triangle AE'F'$，连接 $CE'$，$BF'$，求证：$CE' = BF'$.
（3）在图②的旋转过程中是否存在 $CE' // AB$？若存在，求出相应的旋转角 $\alpha$；若不存在，请说明理由.

答案：
21.
(1)证明:
∵AB=AC,∠A=36°,
∴∠ABC=∠C=72°.
又BE平分∠ABC,
∴∠ABE=∠CBE=36°,
∴∠BEC=180° - ∠C - ∠CBE=72°,
∴∠ABE=∠A,∠BEC=∠C,
∴AE=BE,BE=BC,
∴AE=BC;
(2)证明:
∵AC=AB且EF//CB,
∴AE=AF.
由旋转的性质,得∠EAC=∠F'AB,AE'=AF'.
在△CAE'和△BAF'中,{AC=AB,
{∠E'AC=∠F'AB,
{AE'=AF',
∴△CAE'≌△BAF',
∴CE'=BF'.
(3)解:存在CE'//AB.
理由:由
(1)可知AE=BC,
∴在△AEF绕点A逆时针旋转过程中,E点经过的路径(圆弧)与过点C且与AB平行的直线l 交于M,N两点.
如图，①当点E的对应点E'与点M重合时，四边形ABCM为等腰梯形，
∴∠BAM=∠ABC=72°.又∠BAC=36°,
∴∠α=∠CAM=36°.
②当点E的对应点E'与点N重合时，由AB//l,得∠AMN=∠BAM =72°.
∵AM=AN,
∴∠ANM=∠AMN=72°,
∴∠MAN=180° - 2×72°=36°,
∴∠α=∠CAN=∠CAM+∠MAN=72°.
∴当旋转角为36°或72°时，CE'//AB.