《2025年新目标检测同步单元测试卷九年级数学上册人教版》

19. （13分）某企业设计了一款工艺品，每件的成本是 50 元，为了合理定价，投放市场进行试销. 据市场调查，销售单价是 100 元时，每天的销售量是 50 件，而销售单价每降低 1 元，每天就可多售出 5 件，但要求销售单价不得低于成本.
（1）求出每天的销售利润 $ y $（元）与销售单价 $ x $（元）之间的函数解析式.
（2）销售单价为多少元时，每天的销售利润最大？最大利润是多少？
（3）如果该企业要使每天的销售利润不低于 4000 元，且每天的总成本不超过 7000 元，那么销售单价应控制在什么范围内？（每天的总成本 $ = $ 每件的成本 $ × $ 每天的销售量）

答案： 19.解:
(1)$y=(x−50)[50 + 5(100−x)]=(x−50)(−5x + 550)=−5x²+800x−27500$，
∴每天的销售利润$y$（元）与销售单价$x$（元）之间的函数解析式为$y = −5x²+800x−27500(50\leq x\leq100)$.
(2)$y = −5x²+800x−27500 = −5(x−80)²+4500$，
∵$a = −5＜0$，
∴抛物线开口向下，
∴当$x = 80$时，$y$取得最大值，$y_{最大值}=4500$，即当销售单价为$80$元时，每天的销售利润最大，为$4500$元.
(3)当$y = 4000$时，-5(x−80)²+4500 = 4000，解得$x_1 = 70$，$x_2 = 90$，
∵$a = −5＜0$，
∴当$70\leq x\leq90$时，每天的销售利润不低于$4000$元，由每天的总成本不超过$7000$元，得$50(−5x + 550)\leq7000$，解得$x\geq82$，综上，$x$的取值范围是$82\leq x\leq90$，此时满足条件$50\leq x\leq100$，
∴销售单价应该控制在$82～90$元.

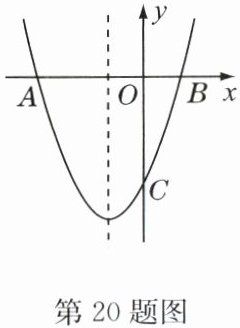
20. （15分）如图，抛物线 $ y = (x + 1)^2 - 4 $ 与 $ x $ 轴交于 $ A $、$ B $ 两点（点 $ A $ 在点 $ B $ 左侧），与 $ y $ 轴交于点 $ C $.
（1）求 $ A $、$ C $ 两点的坐标.
（2）抛物线的对称轴上存在一点 $ P $，使得 $ \triangle PBC $ 的周长最小，求此时点 $ P $ 的坐标及最小周长.
（3）点 $ M $ 是抛物线上一动点，且在第三象限，当四边形 $ AMCO $ 的面积最大时，求出四边形 $ AMCO $ 的最大面积及此时点 $ M $ 的坐标.

答案： 20.解:
(1)令$x = 0$，得$y = −3$，
∴点$C$的坐标为$(0,−3)$.令$y = 0$，则$(x + 1)²−4 = 0$，解得$x = −3$或$x = 1$，
∴$A(−3,0)$.
(2)连接$AC$交对称轴于点$P$，
∵$PB = PA$，
∴$PB+PC = PA+PC$，
∴此时$PB+PC$最短，即$\triangle PBC$的周长最小，设直线$AC$的解析式为$y = kx + b$，则$\begin{cases}b = −3 \\ -3k + b = 0\end{cases}$，解得$\begin{cases}k = −1 \\ b = −3\end{cases}$，
∴直线$AC$的解析式为$y = −x−3$，
∵对称轴为直线$x = −1$，
∴点$P$的坐标为$(−1,−2)$，在$Rt\triangle AOC$中，
∵\angle AOC = 90°$，$OA = OC = 3$，∴$AC = 3\sqrt{2}$，又$BC = \sqrt{OB^{2}+OC^{2}}=\sqrt{1^{2}+3^{2}}=\sqrt{10}$，∴\triangle PBC周长的最小值为$3\sqrt{2}+\sqrt{10}$. (3)连接$OM$，设$M(m,m²+2m−3)$，又$S_{四边形AMCO}=S_{\triangle AOM}+S_{\triangle MOC}=\frac{1}{2}×3×(−m²−2m + 3)+\frac{1}{2}×3×(−m)=-\frac{3}{2}m²-\frac{9}{2}m+\frac{9}{2}=-\frac{3}{2}(m+\frac{3}{2})^{2}+\frac{63}{8}$，∵-\frac{3}{2}＜0$，
∴$m = -\frac{3}{2}$时，四边形$AMCO$的面积最大，最大值为$\frac{63}{8}$，此时点$M(-\frac{3}{2},-\frac{15}{4})$.