《2025年新目标检测同步单元测试卷九年级数学上册人教版》

19. (14分)如图，在平面直角坐标系中，二次函数y=x²+bx+c的图象与x轴交于点A(−1,0)，B(3,0)，与y轴交于点C.
(1)b=-2，c=-3；
(2)若点D在该二次函数的图象上，且S△ABD=2S△ABC，求点D的坐标；
(3)若点P是该二次函数图象上位于x轴上方的一点，且S△APC=S△APB，直接写出点P的坐标.

答案：
19.解：
(1)$\because$点$A$和点$B$在二次函数$y=x^{2}+bx + c$图象上，
$\therefore\begin{cases}0=1 - b + c\\0=9 + 3b + c\end{cases}$解得$\begin{cases}b=-2\\c=-3\end{cases}$故答案为$-2$，$-3$.
(2)如图①，连接$BC$，由题意可得$A(-1,0)$，$B(3,0)$，$C(0,-3)$，$y=x^{2}-2x - 3$，
$\therefore S_{\triangle ABC}=\frac{1}{2}×4×3=6$，
设点$D(m,m^{2}-2m - 3)$，$\because S_{\triangle ABD}=2S_{\triangle ABC}$，
$\therefore\frac{1}{2}× AB×\vert y_{D}\vert=2×6$，即$\frac{1}{2}×4×\vert m^{2}-2m - 3\vert=2×6$，
解得$x=1+\sqrt{10}$或$x=1-\sqrt{10}$，代入$y=x^{2}-2x - 3$，可得$y$值都为$6$，
$\therefore D$点坐标为$(1+\sqrt{10},6)$或$(1-\sqrt{10},6)$.

(3)设$P(n,n^{2}-2n - 3)$，$\because$点$P$在抛物线位于$x$轴上方的部分，$\therefore n＜-1$或$n＞3$，
当点$P$在点$A$左侧，即$n＜-1$时，可知点$C$到$AP$的距离小于点$B$到$AP$的距离，
$\therefore S_{\triangle APC}＜S_{\triangle APB}$，不成立；
当点$P$在点$B$右侧，即$n＞3$时，
$\because\triangle APC$和$\triangle APB$都以$AP$为底，若要面积相等，则点$B$和点$C$到$AP$的距离相等，即$BC// AP$，如图②，
设直线$BC$的解析式为$y=kx + p$，
则$\begin{cases}0=3k + p\\-3=p\end{cases}$解得$\begin{cases}k=1\\p=-3\end{cases}$
则设直线$AP$的解析式为$y=x + q$，将点$A(-1,0)$代入，则$-1 + q=0$，解得$q=1$，
则直线$AP$的解析式为$y=x + 1$，将$P(n,n^{2}-2n - 3)$代入，则$n^{2}-2n - 3=n + 1$，解得$n=4$或$n=-1$（舍），
$\therefore n^{2}-2n - 3=5$，$\therefore$点$P$的坐标为$(4,5)$.

20. (15分)如图，取一副三角板按图①拼接，固定三角板ADE(含30°角)，将三角板ABC(含45°角)绕点A顺时针方向旋转一个大小为α的角度(0°＜α＜180°).
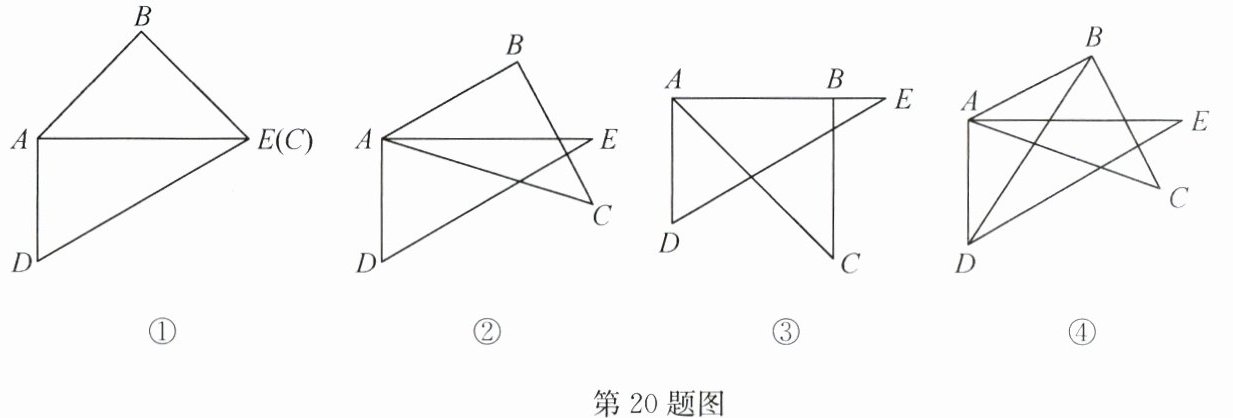
(1)如图②，当α=15°时，指出图中AB与DE的位置关系，并说明理由.
(2)当旋转到AB与AE重叠时(如图③)，则α=45°.
(3)当△ADE的一边与△ABC的某一边平行(不共线)时，直接写出旋转角α的所有可能的度数.
(4)当0°＜α≤45°时，连接BD(如图④)，探求∠DBC+∠CAE+∠BDE是否为一个定值，如果是，求这个定值，并写出解答过程；如果不是，请说明理由.

答案：
20.解：
(1)结论：$AB// DE$.
理由：如题图②，$\because\angle EAC=15^{\circ}$，
$\therefore\angle BAE=45^{\circ}-15^{\circ}=30^{\circ}$，$\therefore\angle BAE=\angle E$，$\therefore AB// DE$.
(2)当旋转到$AB$与$AE$重合时（如题图③），则$\alpha=45^{\circ}$.
(3)当$\triangle ADE$的一边与$\triangle ABC$的某一边平行（不共线）时，所有可能的情况如图①②③④⑤.

①当$AB// DE$时，$\alpha=15^{\circ}$；②当$AD// CB$时，$\alpha=45^{\circ}$；
③当$DE// BC$时，$\alpha=105^{\circ}$；④当$AE// BC$时，$\alpha=135^{\circ}$；⑤当$AC// DE$时，$\alpha=150^{\circ}$.
(4)如图⑥，当$0^{\circ}＜\alpha\leqslant45^{\circ}$时，$\angle DBC+\angle CAE+\angle BDE=105^{\circ}$，保持不变.

理由：设$BD$分别交$AE$，$AC$于点$M$，$N$，在$\triangle AMN$中，$\angle AMN+\angle CAE+\angle ANM =180^{\circ}$，
$\because\angle ANM=\angle C+\angle DBC$，$\angle AMN=\angle E+\angle BDE$，
$\therefore\angle E+\angle BDE+\angle CAE+\angle C+\angle DBC=180^{\circ}$，
$\because\angle E=30^{\circ}$，$\angle C=45^{\circ}$，$\therefore\angle DBC+\angle CAE+\angle BDE=180^{\circ}-75^{\circ}=105^{\circ}$.