1. 如果三角形的一个外角和与它不相邻的两个内角的度数之和为180°,那么与这个外角相邻的内角度数为(
A.30°
B.60°
C.90°
D.120°
C
)。A.30°
B.60°
C.90°
D.120°
答案:
C
2. 如图,P是△ABC内一点,连结BP并延长,交AC于点D,连结PC,则∠1,∠2,∠A的大小关系是(

A.∠A>∠2>∠1
B.∠A>∠1>∠2
C.∠2>∠1>∠A
D.∠1>∠2>∠A
D
)。
A.∠A>∠2>∠1
B.∠A>∠1>∠2
C.∠2>∠1>∠A
D.∠1>∠2>∠A
答案:
D
3. 若三角形的三个外角的度数之比为2:3:4,则与之对应的三个内角的度数之比为(
A.4:3:2
B.3:2:4
C.5:3:1
D.3:1:5
C
)。A.4:3:2
B.3:2:4
C.5:3:1
D.3:1:5
答案:
C
4. 如图,将一把直尺放在一张三角形纸片上,下列结论正确的是(
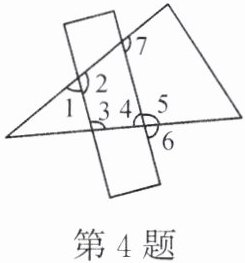
A.∠1 + ∠6>180°
B.∠2 + ∠5<180°
C.∠3 + ∠4<180°
D.∠3 + ∠7>180°
D
)。
A.∠1 + ∠6>180°
B.∠2 + ∠5<180°
C.∠3 + ∠4<180°
D.∠3 + ∠7>180°
答案:
D
5. 如图,已知BC⊥ED,垂足为O,∠A = 27°,∠D = 20°,则∠ACB =
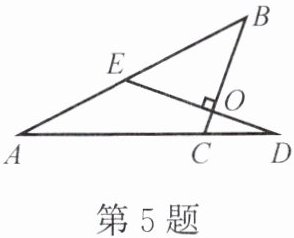
110
度,∠B = 43
度。
答案:
110 43
6. 如图,点A,C,F,B在同一条直线上,CD平分∠ECB,FG//CD。若∠ECA的度数为α,则∠GFB =

$90^{\circ }-\frac {\alpha }{2}$
。(用含α的代数式表示)
答案:
$90^{\circ }-\frac {\alpha }{2}$
7. 补全解题过程。
如图,在△ABC中,∠ABC的平分线BP和外角平分线CP交于点P,试猜想∠A与∠P之间的关系,并说明理由。

解:∠A = 2∠P。理由:
因为BP,CP分别平分∠ABC,∠ACD(已知),
所以∠ABC =
因为∠ACD为△ABC的外角,
所以∠ACD = ∠A + ∠
所以2∠2 = ∠A + 2∠1。
同理,∠2 = ∠P +
所以∠A = 2∠P。
如图,在△ABC中,∠ABC的平分线BP和外角平分线CP交于点P,试猜想∠A与∠P之间的关系,并说明理由。

解:∠A = 2∠P。理由:
因为BP,CP分别平分∠ABC,∠ACD(已知),
所以∠ABC =
2
∠1,∠ACD = 2∠2(角平分线的定义
)。因为∠ACD为△ABC的外角,
所以∠ACD = ∠A + ∠
ABC
= ∠A + 2∠1(三角形外角的性质)。所以2∠2 = ∠A + 2∠1。
同理,∠2 = ∠P +
∠1
。所以∠A = 2∠P。
答案:
2 角平分线的定义 ABC ∠1
查看更多完整答案,请扫码查看


